| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- lateral stability
- annex14
- Turn radius
- 2007년 제4차 자가용조종사 변형
- dutch roll
- directional stability
- Best Glide Speed
- load factor
- sideslip
- FPNM
- 2007년 제3차 운송용조종사 변형
- 국제민간항공협약
- Lead Radial
- 항공안전법
- ICAO Annex 14
- dihedral effect
- UAM
- 13년도 공단 기출문제 변형
- Today
- Total
비행사의 다이어리
'원운동(선회)'에 대해 다시 생각해봅니다. 본문
예전에 착각했던 KEEL AREA 정의에 이어 다시금 충격을 받았습니다. 당연하다고 여겨졌던 것들이, 글을쓰기 위해 정리하다 보면, 틀린 사실이 있다는 것을 알게됩니다. 그렇게 제가 착각하고 있었던 개념중 하나는 원운동에 작용하는 힘에 대한 개념이고 또다른 하나는 바로 원심력에 대한 개념입니다.
먼저, 해당글에서 사이드 슬립과 원운동의 차이를 설명할때 운동방향과 힘이 작용하는 각도의 차이로 포물선 운동과 원운동을 구분하여 설명하려고 하였으나 사실 두가지 운동 모두 근본적으로 원운동의 일종으로 힘이 작용하는 각도차이로는 구분할 수 없음을 간과하였습니다. 일례로 공을 수직으로 던지면 처음에는 공의 진행방향과 중력이 직각을 이루지만 결국은 원운동이 아닌 포물선 운동을 하게 됩니다.

여기서 포물선 운동을 반지름이 줄어드는 원운동으로 볼수 있는데, 속도가 충분하지 않기 때문에 중력을 구심력으로 하는 원운동의 반지름이 매우 작아지고, 그때문에 속도에 맞는 반지름에 도달하기 위해 중력방향으로 떨어지는 것입니다. 극단적으로 공을 거의 수직으로 떨어뜨리면 구심력(중력)에 수직하는 속도는 거의 0가 되는데 원운동의 반지름은 더욱 더 0에 가까워져야 하고 때문에 결국, 반지름을 줄이기위해 공이 수직으로 떨어진다고 생각할 수 있습니다. 물론 떨어지면서 중력에 의해 속도가 가속되어 결과적으로는 원운동이 아니라 타원운동을 하게 됩니다. 어떻게 보면 너무나도 당연한 이야기인데 저는 이걸 이제야 제대로 이해하였습니다(-_-;;).
 |
 |
따라서 포물선 운동과 원운동의 개념으로는 사이드슬립과 원운동의 차이를 설명할 수 없기 때문에 해당설명은 당연히 철회하였습니다.
또 하나의 중대한 실수는 원심력은 관성력이라 무조건 관성력을 만들어내는 힘이랑 100% 일치해야 한다는 사실을 간과한 것입니다. 사실 이 오류도 비행기의 선회에 관한 글을 쓸때까지도 전혀 자각하지 못하였으나 이후 관성력을 다루는 하중계수에 대한 글을 작성하면서 논리적으로 뭔가 이상한 낌새를 차리고 알게 되었습니다. 사실 대단한 것도 아니고 이것 또한 고등학교 물리 수준의 개념이었는데 말이죠.
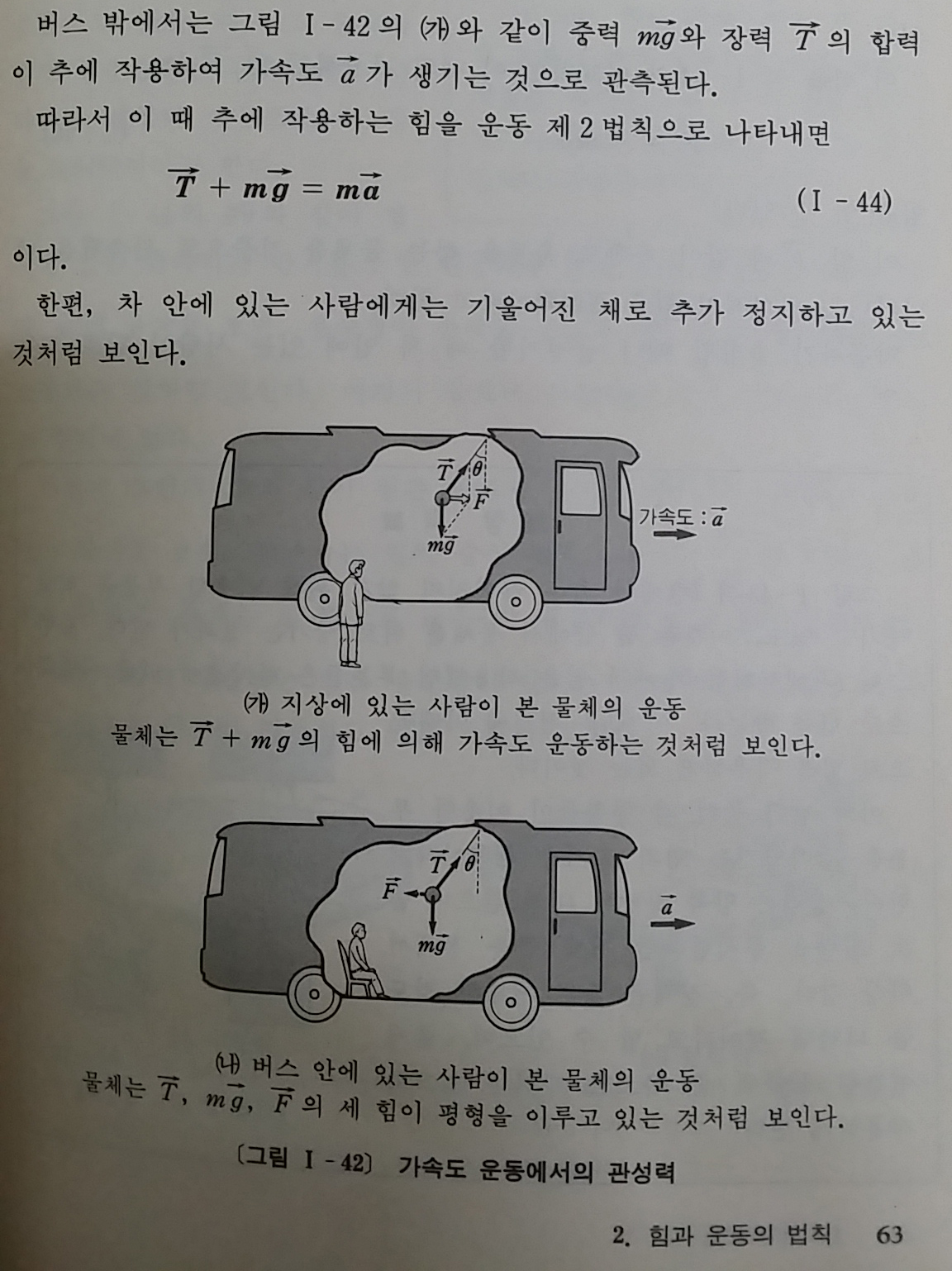
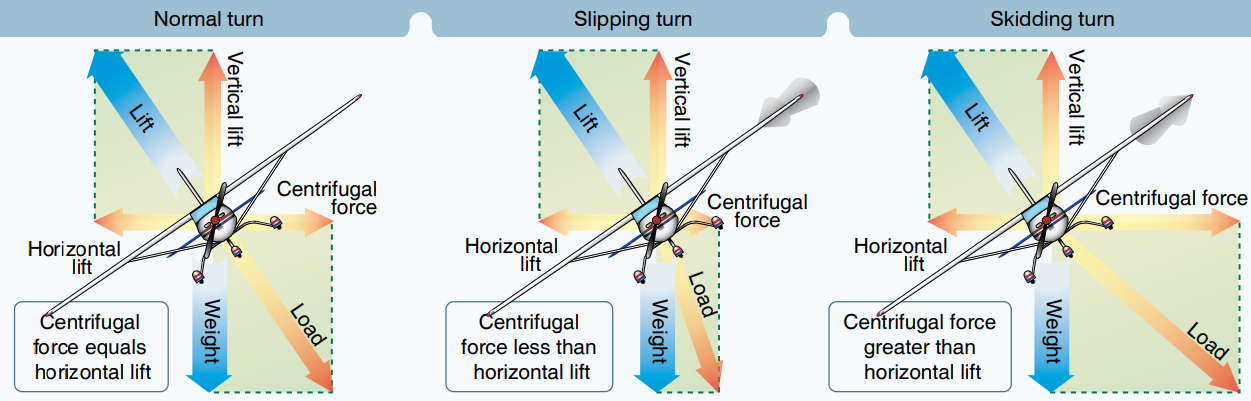
그 원인은 사실 PHAK을 잘못 이해한 부분이 없지 않았습니다. PHAK에서는 SLIP과 SKID가 양력의 수평성분과 원심력의 크기 차이에서 비롯된다고 설명하는데, 저는 아주 자연스럽게 양력의 수평성분을 구심력으로 간주해 버렸습니다. 그리고 아무리 벡터분해를 해보아도 맞지 않는 것이 하도 이상하였으나 열심히 끌어다 맞추어 보니 얼추 맞는 것 같아 보였습니다. 사실 이게 자기 자신도 속여버리는 제일 위험한 실수인데 해버린 것이죠. 또다시 스스로 반성합니다.
이래서 독학이 위험합니다. 그래서 제가 블로그를 하는것도 다른 사람들에게 알려주기 위한 목적도 있지만 제가 알고있는 사실들을 다른 사람들이 알고 있는 사실들과 교차검증하기 위한 목적이 큽니다. 그러니 오류나 이상한 점이 있으면 언제든지 알려주세요. 그래서 댓글이나 방명록 모두 로그인 없이 아무나 달수 있도록 해 놓았습니다. 저도 열심히 노력은 하고 있으나 사람인지라 계속 실수가 나옵니다.
어째든, 다시 원심력으로 돌아와서, 원심력은 관성력이므로 절대로 단독으로 나타날 수 없습니다. 반드시 그에 상응하는 힘이 필요합니다. 그런데 slipping 선회일때는 양력의 수평성분보다 원심력이 작아지고 skidding 선회일때는 양력의 수평성분보다 원심력이 커집니다. 이말은 즉 slipping 선회는 정상 선회일때 보다 구심력이 작고 skidding 선회는 정상 선회일때 보다 구심력이 크다는 이야기입니다.
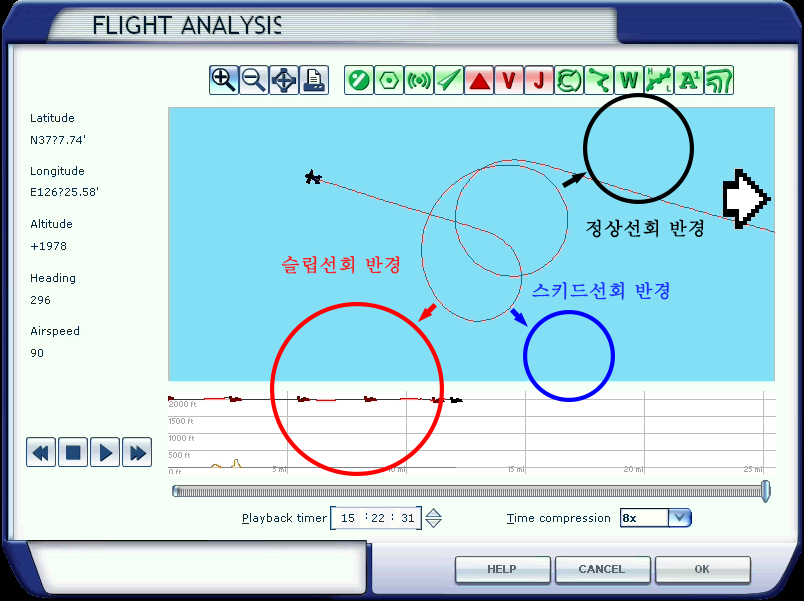
솔직히 고백하자면 저는 이 오류를 발견하기 전까지 slipping 선회일때는 선회 반지름이 나선형으로 점점 작아지고 skidding 선회일때는 선회 반지름이 나선형으로 점점 커진다고 생각했습니다. 원심력을 양력의 수평성분에 영향을 미치는 개별적인 힘으로 생각했기 때문입니다. 다시 말씀드리지만 이것은 명백한 오류입니다.
slipping 선회일때는 구심력이 작기 때문에 정상 선회때 보다 선회 반지름이 큰 원을 그리게 됩니다. 그리고 skidding 선회일때는 구심력이 크기 때문에 정상 선회때 보다 선회 반지름이 작은 원을 그리게 됩니다. 이것을 MS Flightsimulator X로도 검증해본 결과도 일치하였습니다.
하지만 대체 왜 구심력이 감소하고 증가하게 되는지 그 원인을 찾지 못하고 있었습니다. 다만 러더가 관성력에 영향을 미친다고만 막연히 추측할 따름이었습니다. 그렇게 거의 한달 가까이 흘러갈쯤, 항공기쪽에서는 도저히 힌트를 못찾다가 선박쪽에서 그 힌트를 찾을수 있었습니다. 선박은 오로지 러더 하나만 가지고 선회를 하는데 이 러더에서 에어포일에서 양력에 해당하는 힘이 구심력을 발생시키는 것이었습니다.
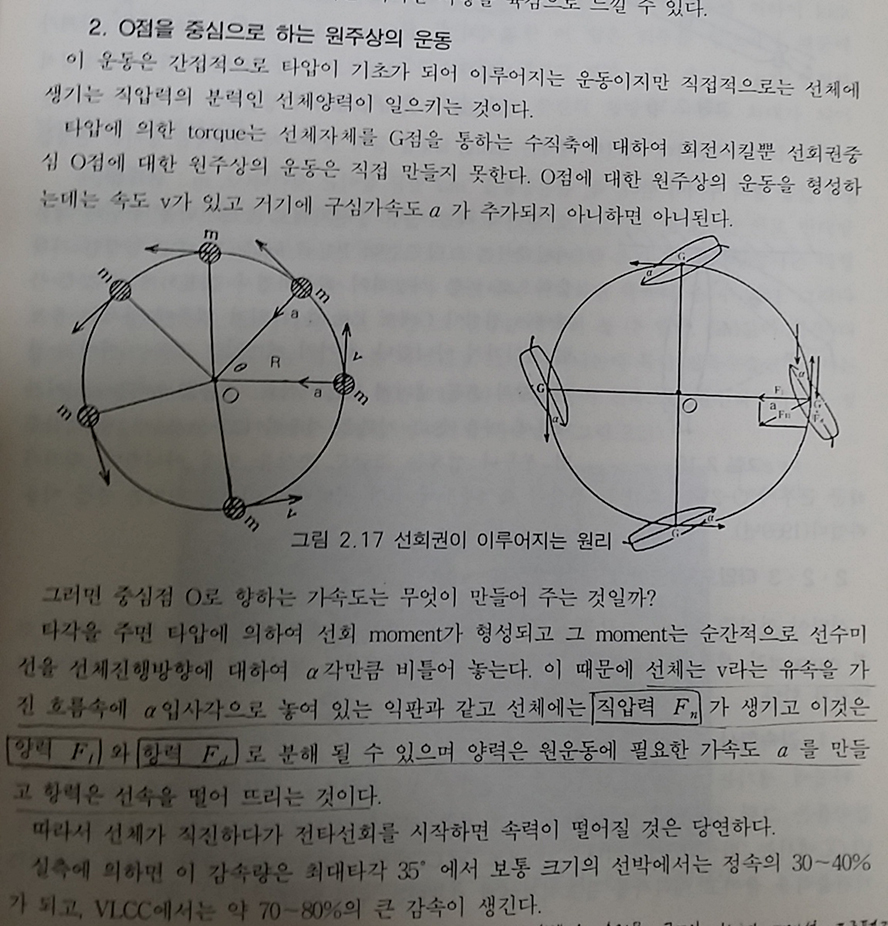
비행기에서도 적용되는지 MS Flightsimulator X로 구현해본 결과 비행기도 선박처럼 러더로만 선회가 가능했습니다. 즉, 비행기의 러더에서도 구심력이 나타날수 있다는 것을 확인했습니다.
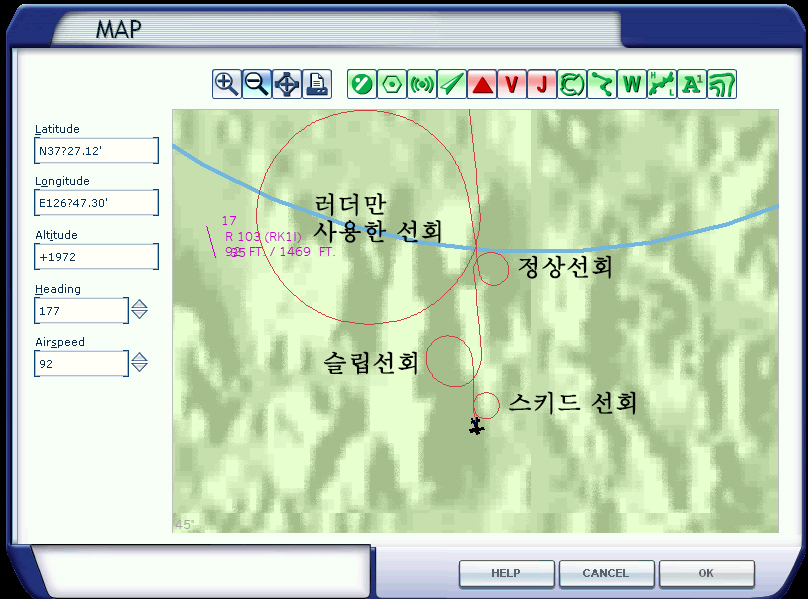
이렇게 러더로 발생하는 구심력을 고려하자 선회에서의 원심력에 대한 문제가 마법같이 모두 해결되었습니다!
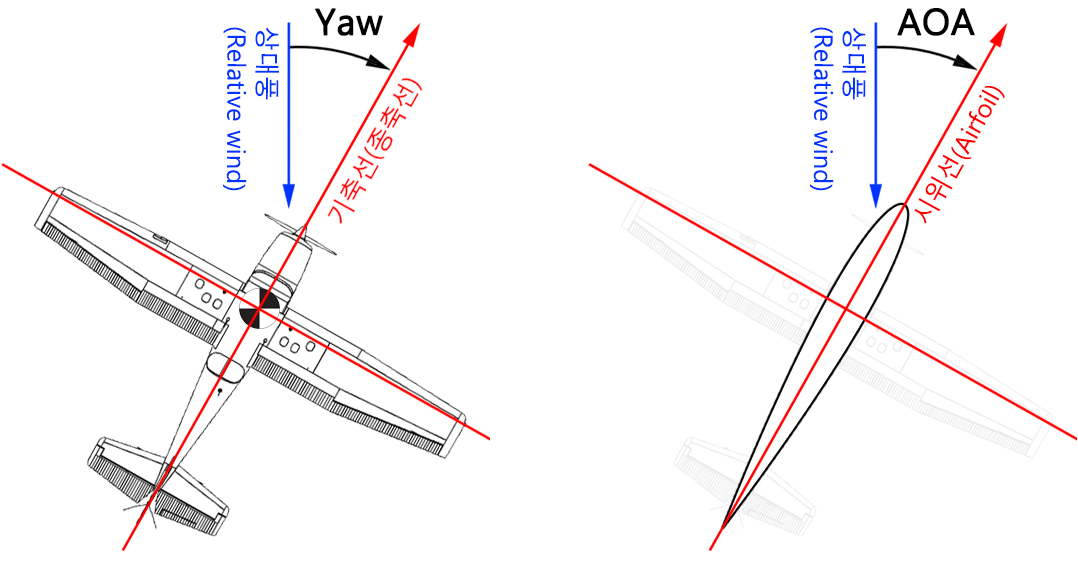
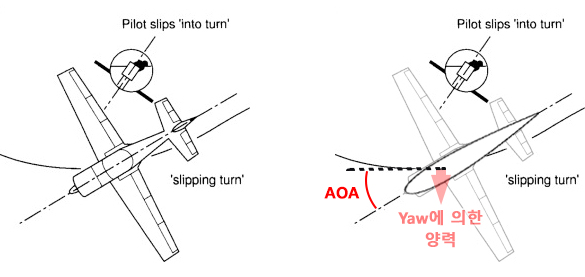
현재 오류가 있었던 '비행기의 선회비행기동에서의 공력학적 힘 (선회) -1' 글은 모두 수정을 완료하였습니다. 만약에 혹시나 제가 오류를 수정하여 설명한 부분에도 오류나 문제가 있으면, 언제든지 편하게 알려주시면 감사하겠습니다.
참고로 수정전 심각한 오류가 있던 원본 글은 반면교사로 삼기위해 밑에 박제해 놓았습니다. -_-
비행기의 선회비행기동에서의 공력학적 힘 (선회) - 1
 |
 |
고체 위를 달리는 자동차나 액체 위를 떠다니는 배와 달리 기체속에서 움직이는 비행기는 러더를 사용해 기수의 방향을 바꾸어도 공기중을 계속해서 미끄러져(slip) 나아갈 뿐 운동 방향이 크게 변하지 않습니다.

따라서 비행기는 주로 날개의 양력을 이용하여 운동 방향을 변화시킵니다.

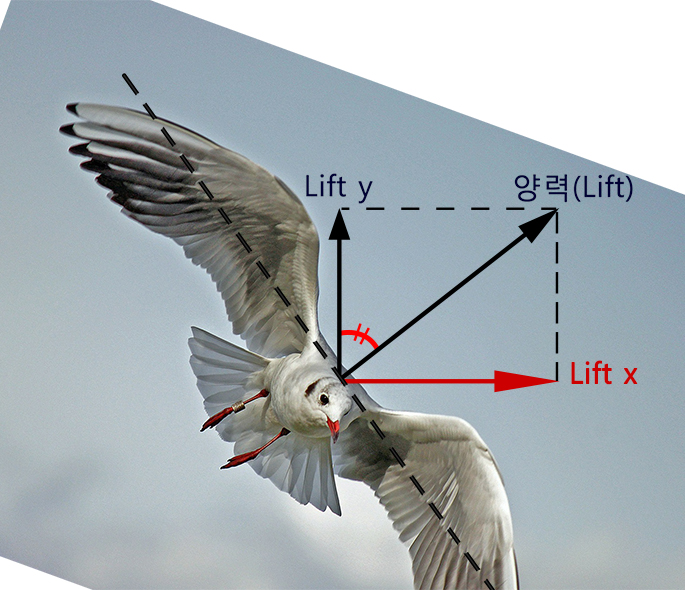
기울어진 양력
비행 중 날개가 기울어지면(bank), 거기서 발생하는 양력도 기울어지게 됩니다. 그리고 이렇게 기울어진 양력의 일부는 수평방향으로 작용하는 힘(Lift x)을 만들어 내게 됩니다.
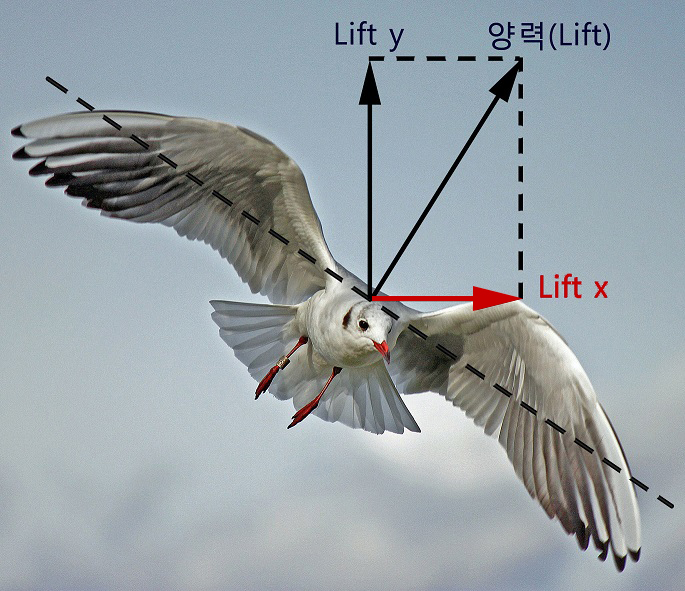
이 양력의 수평성분(Lift x)은 비행기의 운동 방향과 비스듬하게 작용하여 '사이드슬립(side-slip)'을 하게 하거나, 비행기의 운동 방향에 직각으로 작용하여 '선회(turn)'를 하게 합니다.
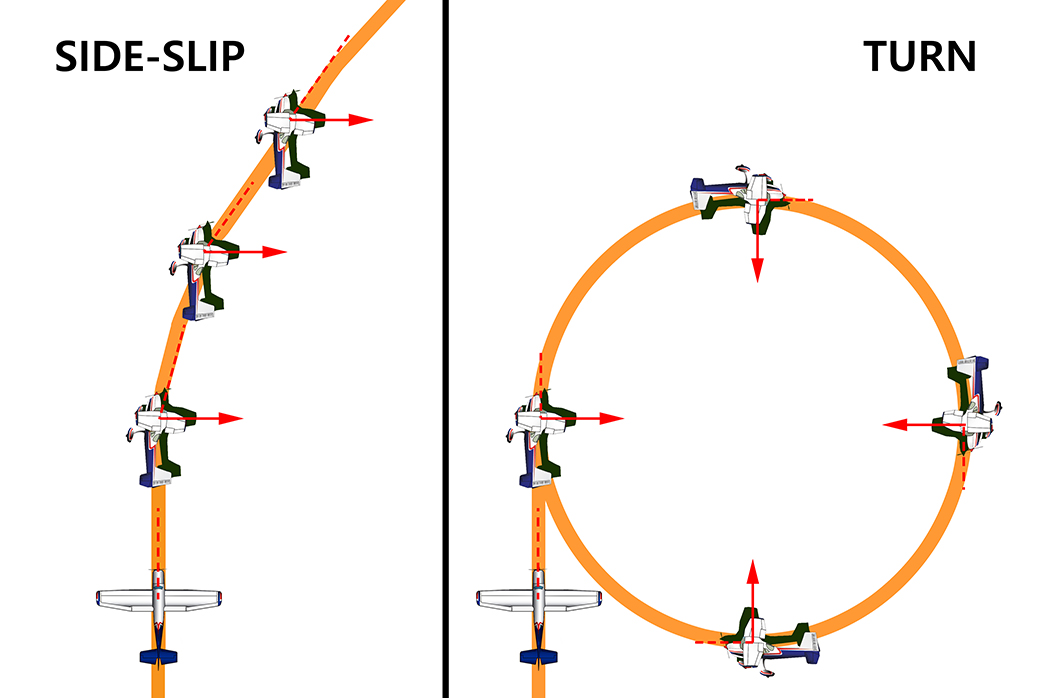
일반적으로 비행기는 상대풍을 추종하는 특성인 '방향안정성'을 가지고 있기 때문에 날개를 기울이게(bank) 되면 사이드슬립 보다는 주로 선회를 하게 되는 경향이 있습니다.
비행기의 선회와 원운동
비행기의 선회는 일종의 '원운동' 입니다.
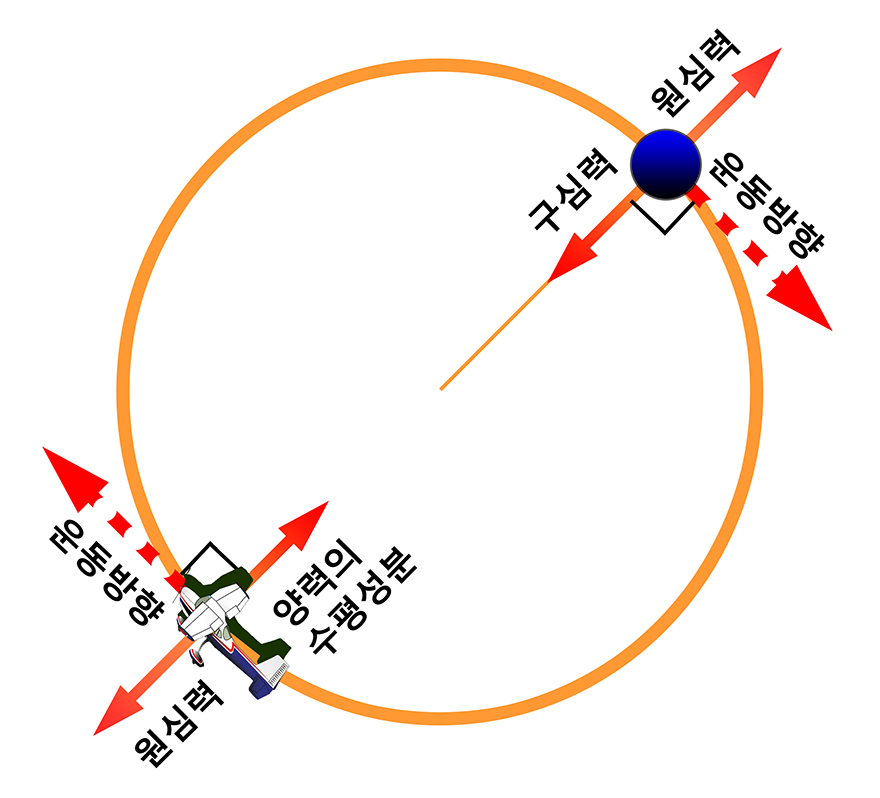
비행기가 선회를 하게 되면 양력의 수평성분이 비행기의 운동 방향과 수직으로 작용하여 '구심력(Centripetal force)'이 되고, 그러한 구심력에 대한 관성력으로서 '원심력(Centrifugal force)'이 나타나게 됩니다.
그리고 이러한 구심력과 원심력이 서로 평형을 이룰 때 비행기는 반지름이 일정한 원운동을 하게 됩니다.
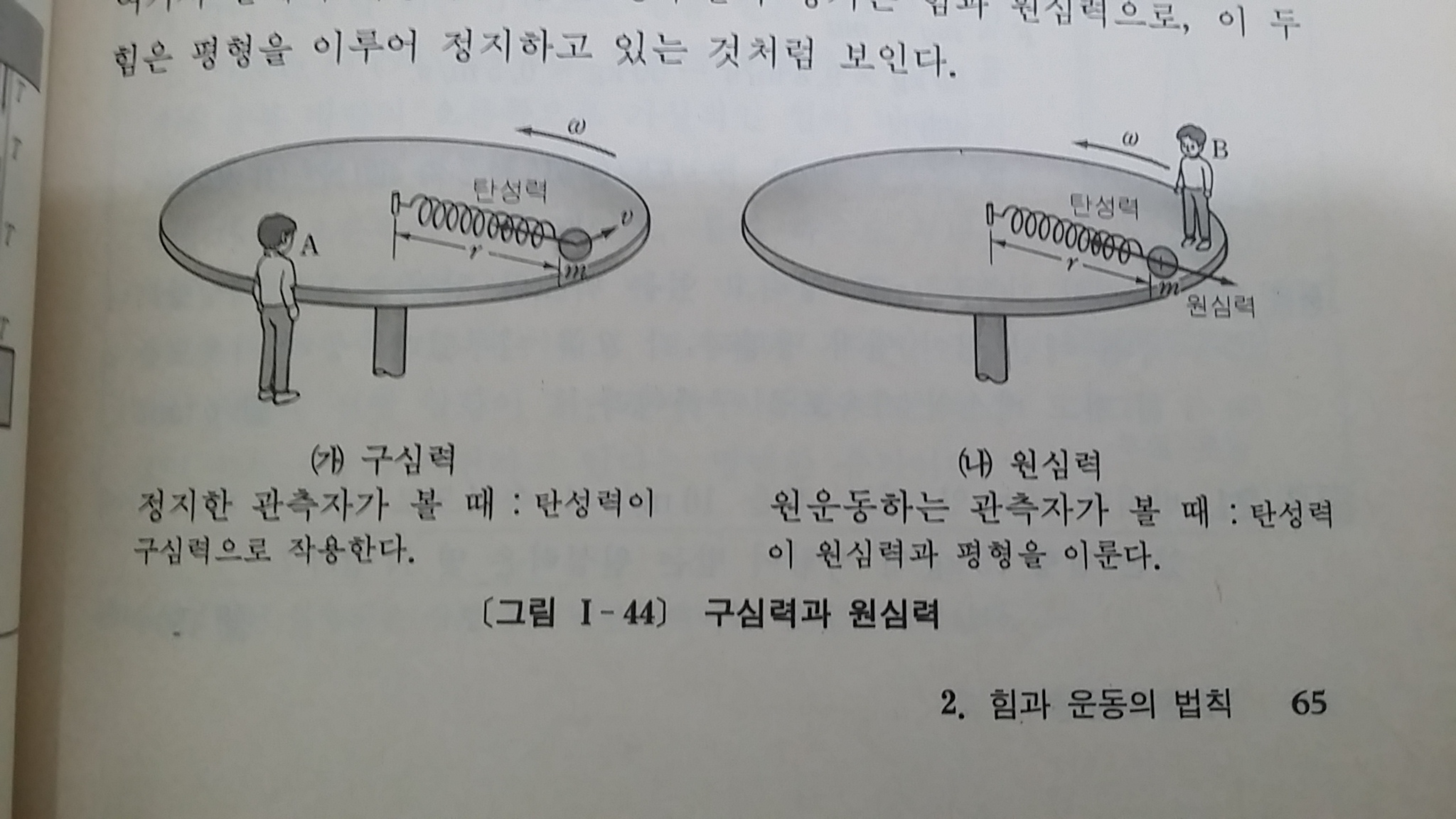
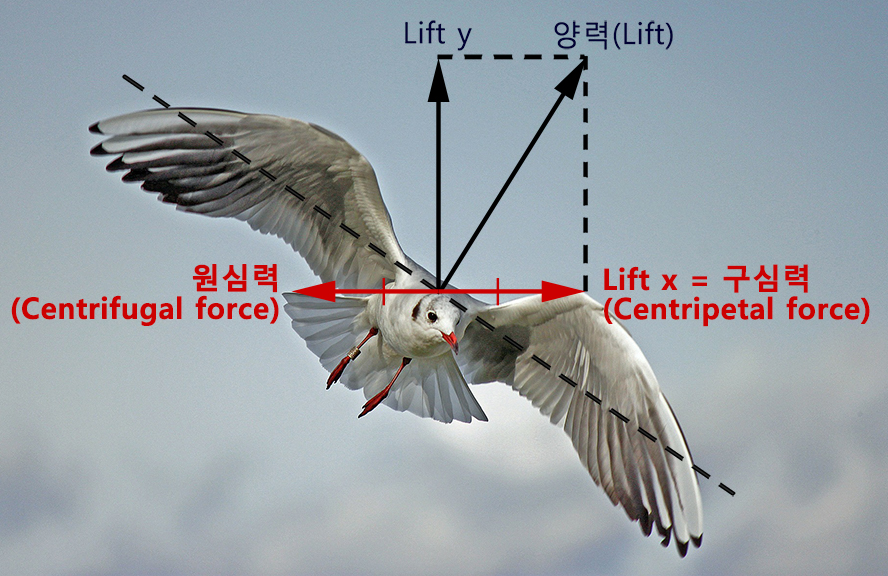
구심력과 원심력
여기서 구심력은 앞에서 살펴보았듯이 양력의 수평성분이기 때문에 날개가 급하게 기울어질수록 커지게 되며,
 |
 |
원심력의 크기는 비행기 속력의 제곱에 비례하고 선회 반지름의 크기에 반비례 하는데요.

정상적인 선회에서는 구심력과 원심력의 크기는 항상 같습니다.
선회 반지름(Turn radius)
따라서 만약 비행기가 구심력이 일정한(bank가 일정한) 선회를 할 때 속력이 증가하게 되면 원심력이 커질수도 있다고 생각할 수 있겠지만, 동시에 선회 반지름도 증가하기 때문에 결과적으로는 원심력이 증가하지 못하고 구심력과 계속 힘의 평형을 이루게 됩니다.
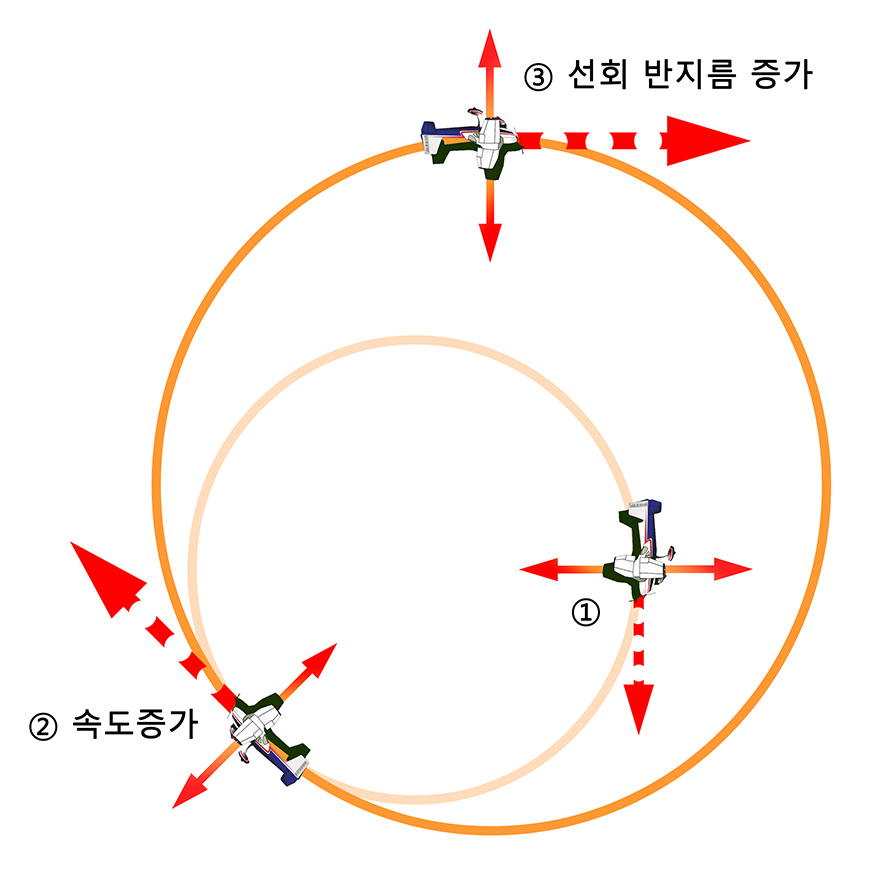
반대로 비행기 속력이 일정한 선회를 할 때 구심력이 증가하게(bank가 증가하게) 되면, 동시에 선회 반지름이 감소하여 결과적으로는 원심력이 증가하여 구심력과 계속 힘의 평형을 이루게 됩니다.
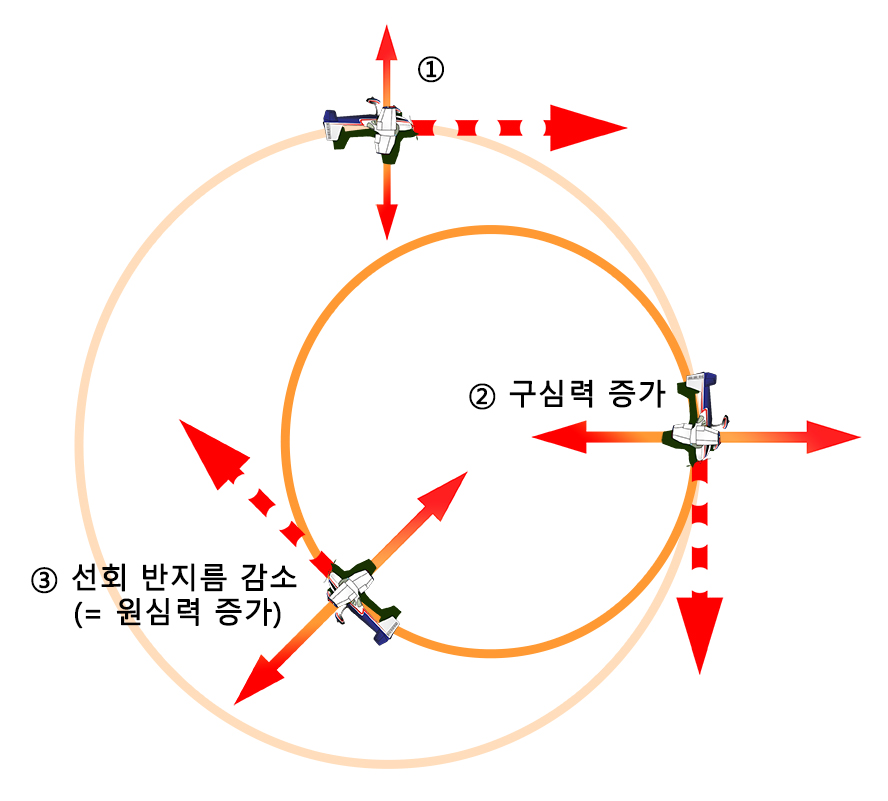
이처럼 '구심력을 만드는 날개 기울기'와 '원심력에 영향을 미치는 비행기의 속력'은 선회 반지름을 결정합니다.
그리고, 날개의 기울기 와 비행기의 속력은 선회율에도 영향을 미치게 되는데요.
선회율(Rate of Turn, ROT)
'선회율'이란 비행기의 선수방위(heading) 각도의 변화율을 말하며 일반적으로 1초 동안 변화한 각도로 나타냅니다. 즉, 각속도의 개념으로, 선회 반지름의 크기와 상관없이 비행기가 얼마나 빨리 한 바퀴를 돌 수 있는지를 알려줍니다.
앞서 원심력의 크기가 비행기 속력의 제곱에 비례하고 선회 반지름의 크기에 반비례 한다고 하였는데요.

이 것을 원심력과 각속도의 관계로 나타내보면(고등학교 물리 -_-;;),
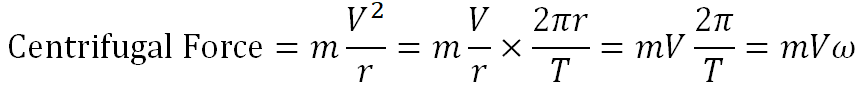
원심력이 일정할 때 속력이 증가하면 선회율(각속도)은 오히려 떨어지게 된다는 것을 알 수 있습니다.
사실 속력이 증가하면 반지름은 증가한 속력의 제곱으로 커져야 원심력이 유지가 되기 때문에 속력의 증가량보다 이동해야하는 거리 증가량이 훨씬커져서 선회율은 오히려 떨어지게 됩니다. 만약 이렇게 속력이 증가하는 상황에서 선회율을 유지려면 bank를 증가시켜(구심력 증가) 선회 반지름이 너무 커지지 않도록 해야합니다.
선회 중 고도유지의 문제
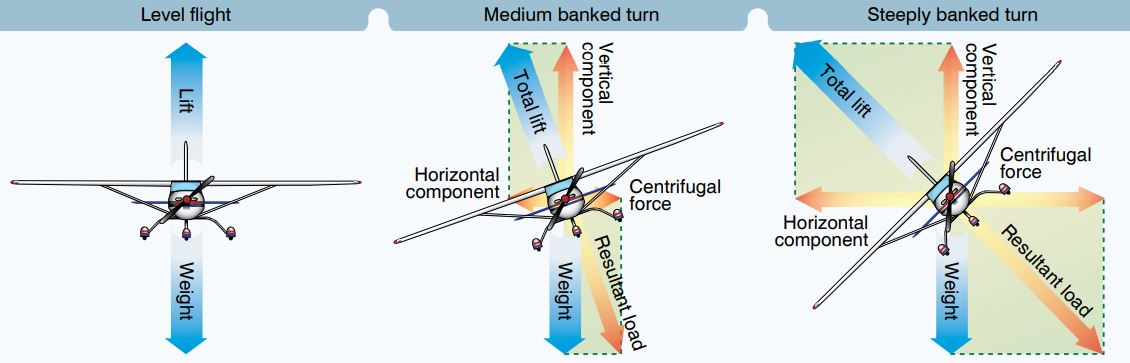
그런데, 선회를 하기 위해 단순하게 날개에 bank를 주어 양력의 수평성분을 만들어내게 되면 비행기 무게(Weight)를 지탱하는 양력의 수직성분(Vertical component)이 그만큼 작아지기 때문에 고도를 유지할 수 없게 됩니다. 따라서 선회시 고도를 유지하려면 직진수평비행을 할 때보다 더 많은 양력이 필요합니다.
그래서 선회를 할 때는 '받음각(Angle of attack)'을 증가시켜서 전체적인 양력(Total lift)이 충분히 커지도록 하여 양력의 수직성분이 비행기의 무게를 감당할 수 있도록 해야 합니다.
 |
 |
그런데 이렇게 받음각이 증가하게 되면 필연적으로 '유도항력'이 증가하게 되어 속력을 잃게 됩니다. 따라서 선회를 할 때는 직진수평비행을 할 때보다 더 많은 추력이 요구됩니다.
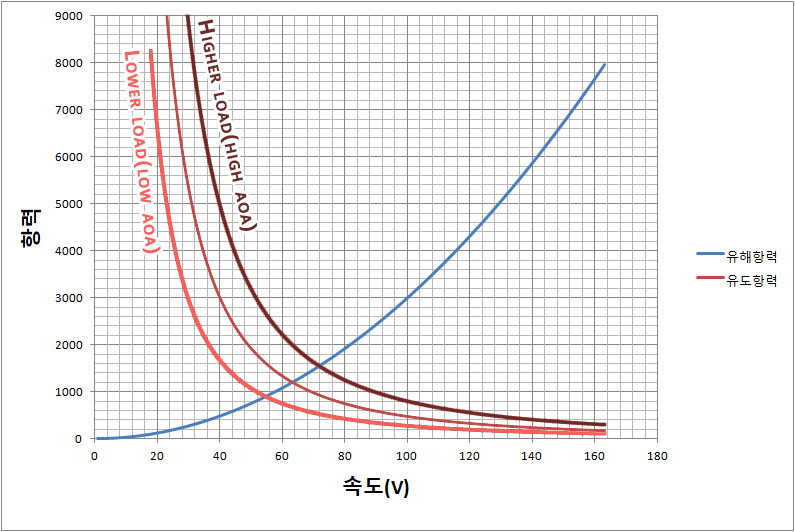
하중계수(Load factor)

선회시 고도유지를 위해 전체 양력을 증가시키면 자연히 양력의 수직성분 뿐 아니라 수평성분으로 작용하는 구심력도 같이 증가하기 때문에 관성력으로 작용하는 원심력이 증가하게 됩니다.
이렇게 증가한 원심력에 중력(=비행기의 무게)이 더해지면 실제로 느끼게 되는 비행기의 무게는 더욱 커지게 됩니다.
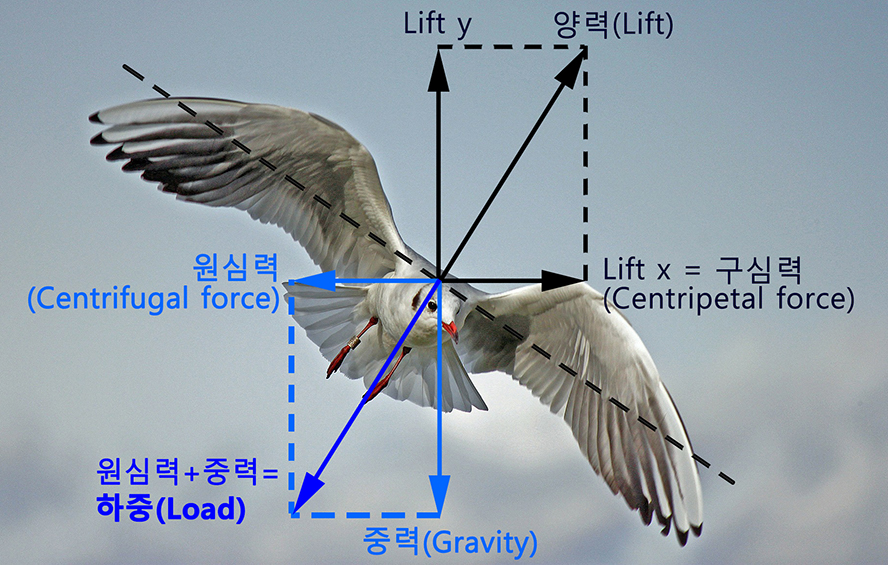
이처럼 원심력에 중력이 더해진 힘을 '하중(Load)'이라고 하며 하중의 크기는 비행기의 전체 양력과 항상 같습니다.
따라서 하중을 측정하는 방식인 하중계수(Load factor)는 '비행기 총 무게에 대한 전체 양력의 비율'로 측정하며 단위는 중력가속도(G-force)를 나타내는 'G'를 사용합니다. 가령, 1G는 직진수평비행을 할 때와 같이 비행기의 무게와 양력이 같을 때이며, 2G는 양력, 즉 하중이 비행기 무게의 2배가 됨을 나타냅니다.
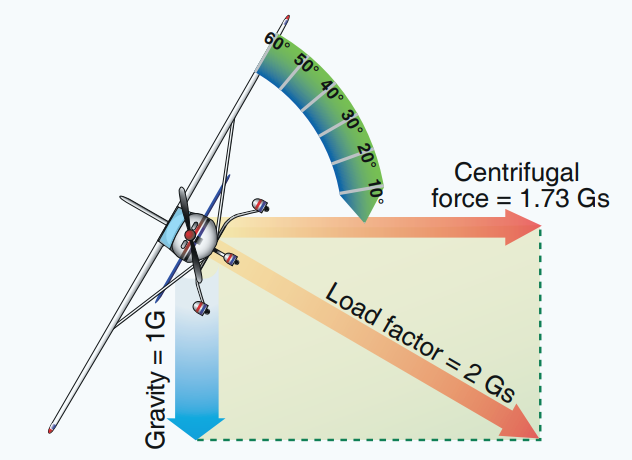
참고로 비행기가 60도 bank로 고도 변화 없이 선회를 하게 되면 2G의 하중을 받게 됩니다.
선회 중 YAWING 이 나타날때
선회 중 양력의 수평성분이 운동 방향에 직각이 아니게 될 때
앞서 양력의 수평성분(Lift x)이 비행기의 운동 방향과 비스듬하게 작용하면 '사이드슬립(side-slip)'을, 비행기의 운동 방향에 직각으로 작용하면 '선회(turn)'를 하게 된다고 하였습니다.

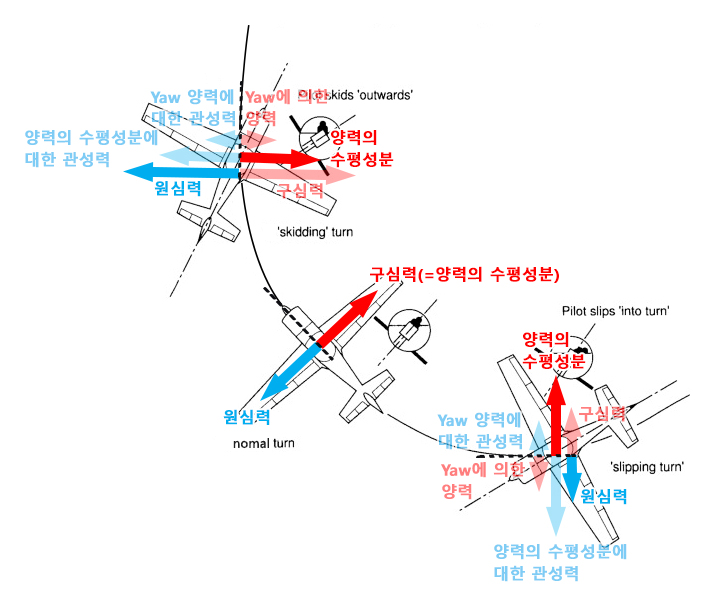
만약 비행기의 방향안정성이 완벽하다면 양력의 수평성분은 비행기의 운동방향에 항상 수직하게 나타나기 때문에 이상적인 원운동을 할 수 있지만, 현실에서는 여러가지 이유들로 인해 비행기의 방향안정성이 100% 완벽할 수는 없습니다. 따라서 사이드슬립은 아니지만 완벽한 원운동도 아닌 애매한 형태의 선회가 나타날 수 있는데 바로 'Slipping 선회' 와 'Skidding 선회' 입니다.
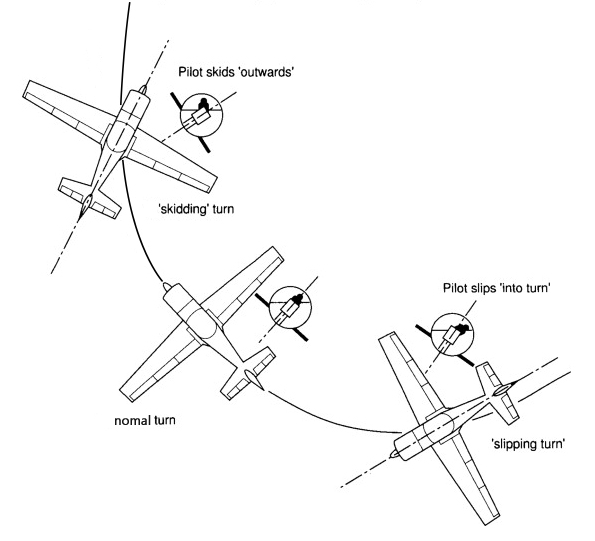
Slipping 선회
Slipping 선회는 기수가 선회경로 바깥쪽으로 돌아간(yaw) 상태를 말합니다.
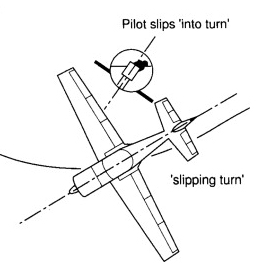
이와같은 현상은 bank로 나타나는 상대풍의 변화가 기수 변화보다 빠를 때 발생하게 됩니다. 즉, 달리 표현하면 bank를 준 것에 비해 선회율(ROT)이 안나오는 현상입니다.
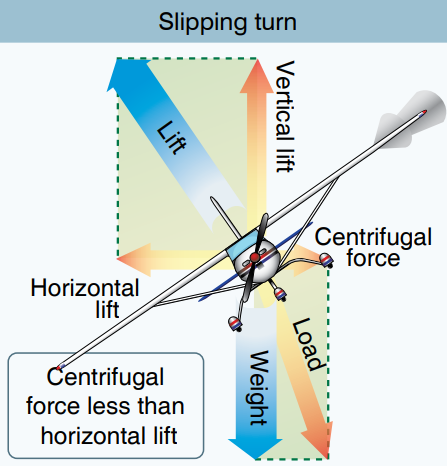
따라서 bank로 인한 양력의 수평성분이 상대적으로 강하기 때문에 구심력이 원심력보다 강하게 나타나며, 아래 그림처럼 비행기의 진행방향과 양력의 수평성분이 직각을 이루지 못하고 직각보다 작은 소각도를 이루게 됩니다.
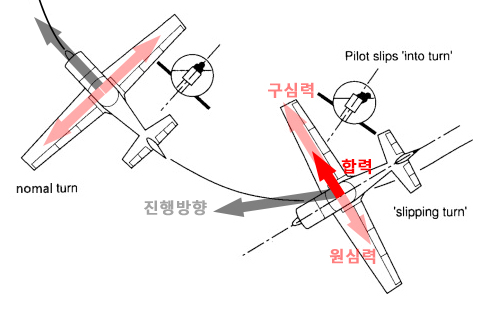
결국 약간의 선회와 더불어 비행기는 원운동을 하지 못하고 비스듬하게 나가게 됩니다.
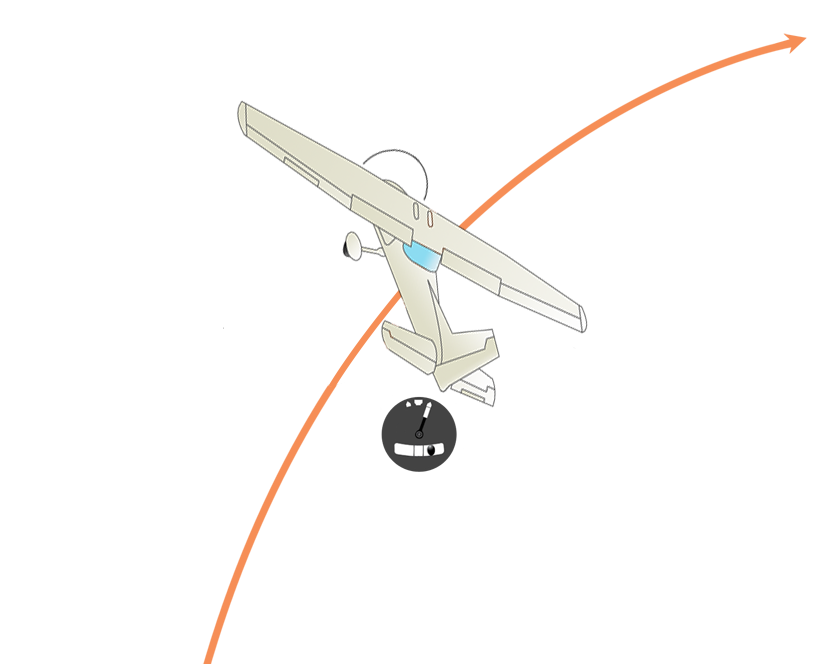
어떻게 보면 사이드슬립과 비슷하지만 기수의 방향이 일정한 사이드 슬립과 달리 Slipping 선회는 기수의 방향이 계속해서 변한다는 차이가 있습니다.
Slipping 선회에서 벗어나려면 bank를 줄이던가, 선회율을 증가 시키던가, 아니면 두가지 방법 모두를 사용해서 비행기를 다시 상대풍에 추종하게 하여 구심력과 원심력을 평형상태로 되돌려 놓아야 합니다.
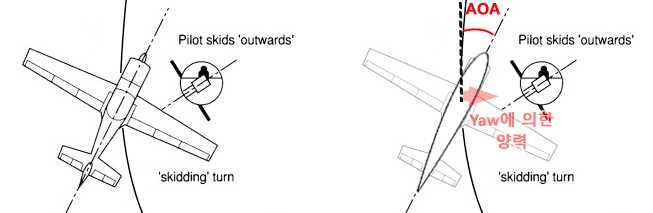
Skidding 선회
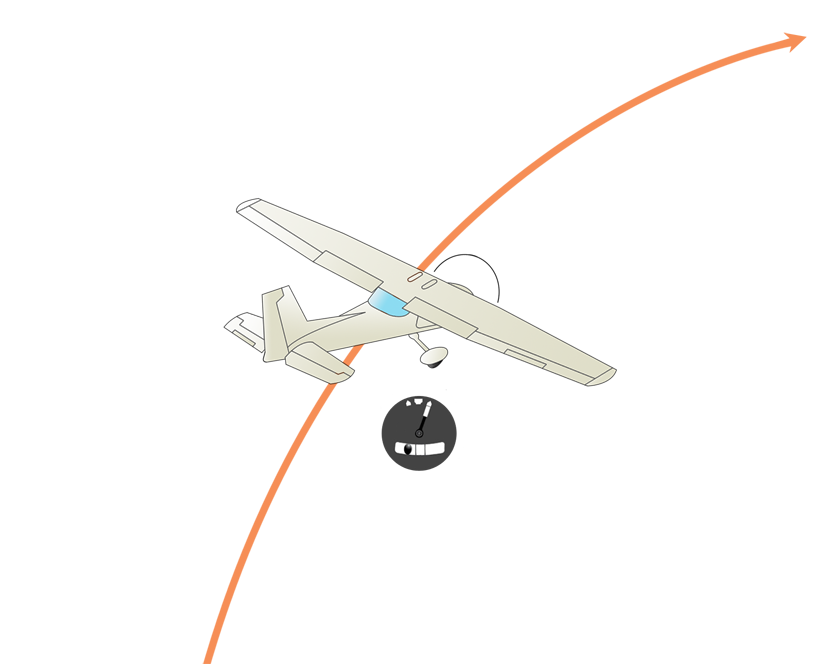
Skidding 선회는 기수가 선회경로 안쪽으로 돌아간(yaw) 상태를 말합니다.
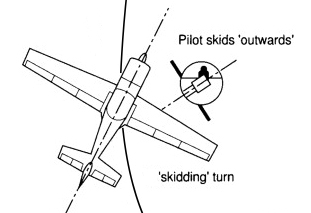
이와같은 현상은 bank로 나타난 상대풍의 변화보다 기수의 변화가 빠를 때 발생하게 됩니다. 즉, 달리 표현하면 bank를 준 것에 비해 선회율(ROT)이 더 나오는 현상입니다.
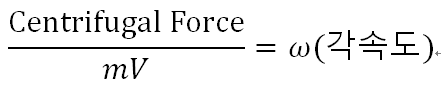
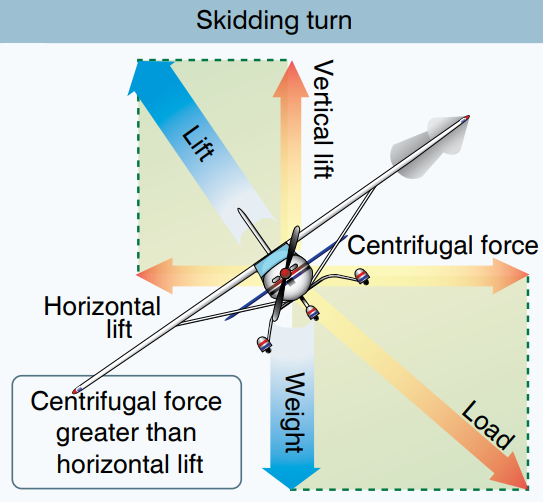
정상적인 선회보다 선회율이 더 나온다는 것은 bank로 만들어내는 구심력보다 원심력이 강하다는 것을 의미하며, 아래 그림처럼 비행기의 진행방향과 양력의 수평성분이 직각을 이루지 못하고 오히려 원심력쪽으로 치우쳐져 원심력과 소각도를 이루게 됩니다.

결국 비행기는 과도한 기수변화와 함께 원운동을 하지 못하고 흡사 자동차의 관성드리프트처럼 밖으로 밀려나며 돌게 됩니다.

Skidding 선회에서 벗어나려면 bank를 증가 시키던가, 선회율을 줄이던가, 아니면 두가지 방법 모두를 사용해서 비행기를 다시 상대풍에 추종하게 하여 구심력과 원심력을 평형상태로 되돌려 놓아야 합니다.
선회에서 구심력과 원심력의 평형이 깨지게 되는 원인은 다양합니다. 다양한 원인들이 있기 때문에 비행기가 가진 방향안정성만으로는 선회경로를 유지하는데 한계가 있습니다. 따라서 조종사는 '러더(rudder)'를 사용하여 선회를 보조해야 합니다.
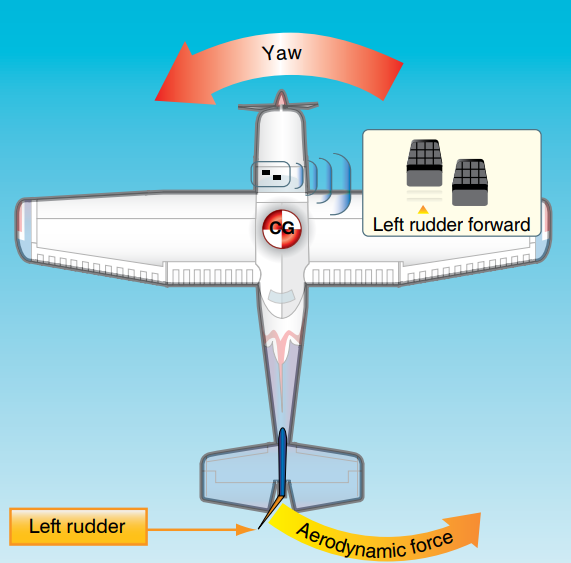
러더 자체로는 비행기의 경로자체를 바꾸기는 어렵지만 일정각도 내에서 비행기의 기수의 방향을 조종할 수 있습니다(yawing). 따라서 러더는 선회 중 상대풍으로 부터 틀어진 기수를 바로잡아 선회율을 조절하고, 이를 통해 구심력과 원심력의 균형을 잡는데 사용해야 됩니다.
'개념 오류 다이어리' 카테고리의 다른 글
| Free Directional Oscillations(Dutch Roll)를 다시 생각해 봅니다. (0) | 2022.01.25 |
|---|



