| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- lateral stability
- 국제민간항공협약
- dihedral effect
- Turn radius
- load factor
- ICAO Annex 14
- directional stability
- 2007년 제3차 운송용조종사 변형
- annex14
- UAM
- sideslip
- FPNM
- Best Glide Speed
- 13년도 공단 기출문제 변형
- 2007년 제4차 자가용조종사 변형
- 항공안전법
- Lead Radial
- dutch roll
- Today
- Total
비행사의 다이어리
비행기동에서의 공력학적 힘 (상승, 강하) - 2 본문
비행기의 상승과 강하도 선회와 마찬가지로 양력을 변화시켜 비행기의 비행방향을 바꾸면서 이루어지게 됩니다. 그리고 일단 비행방향이 상승 또는 강하하는 방향으로 바뀌게 되면, 다시 양력은 수평비행을 할 때와 거의 동일하게 돌아와야 일정한 각도로 상승 또는 강하를 할 수 있습니다.
비행기의 상승(Climb)
직진수평비행에서 상승비행으로 전환하기 위해서는 제일먼저 양력이 증가하여야 합니다. 중력보다 큰 양력은 항공기를 위로 가속시키게 되며 직진경로를 상승경로로 변화시키게 됩니다.

그리고 일단 원하는 상승경로로 진입하고 나서는 양력을 다시 감소시켜 직진수평비행을 할 때와 마찬가지로 힘의 평형을 유지시켜야 합니다.

만약 계속 증가된 양력을 감소시키지 않고 유지하거나 더 증가시키게 되는 경우, 궁극적으로는 아마, 루프(Loop)기동과 비슷한 형태로 위쪽으로 한바퀴 돌게 될 것입니다.
 |
 |
물론 이것은 추력이 월등한 비행기에만 해당될 것이며 일반적인 비행기의 경우에는 그 전에 속력이 감소하여 실속(stall)에 들어갈 수 있기 때문에 왠만큼 빠른 속도로 진입하지 않는 이상 위로 한바퀴 도는 일까지는 없을 것 입니다. 왜냐하면 중력이 항력처럼 작용하기 때문입니다.
상승 중 항력으로 작용하는 중력

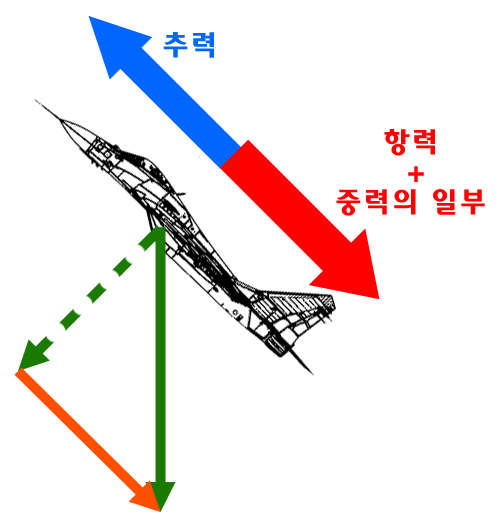
비행기의 상승은 마치 비탈길을 오르는 것과 같기 때문에 힘, 즉 추력(thrust)이 수평비행을 할 때 보다 더 많이 필요하게 됩니다. 그 이유는 이전 글에서도 계속 설명했듯 상승 중에는 중력(무게)의 일부가 항력처럼 작용하기 때문입니다.
 |
 |
따라서 동일한 속력을 계속 유지하기 위해서는 수평비행을 할때 보다 더 많은 추력이 필요하게 되며, 만약 추력을 보충하지 않으면 비행기의 속력은 전체항력이 추력과 같아질 때까지 줄어들게 됩니다.

이처럼 비행기의 상승은 수평비행을 하기위한 추력보다 더 많은 추력, 남는 추력, 즉 소위 잉여추력(Excess thrust)에 의해서 이루어 지며, 이러한 잉여추력이 항력으로 작용하는 중력을 얼마만큼 감당할 수 있느냐에 따라서 비행기의 상승각이 달라지게 됩니다.

가령 비행기가 10도 상승각으로 상승할 때 잉여추력은 비행기 무게의 17%를 감당해야하고, 아주 극단적인 수직상승의 경우 잉여추력은 비행기 전체 중량을 감당해야 합니다.
일반적으로 고도가 상승하면 대기가 희박해지는 이유등으로 잉여추력은 감소하게 되는데, 잉여추력이 0가 되어 더이상 상승하지 못하는 고도를 "절대상승한계고도(Absolute ceiling)"라고 합니다.

힘의 평형(심화학습)
비행기의 상승 또한 속력과 방향이 일정한 등속 직진운동이기 때문에 비행기에 작용하는 모든 힘은 서로 평형을 이루고 있습니다.

위 그림처럼 비행기가 일정한 각도(θ)로 상승할 때, 추력은 항력과 중력의 일부를 감당해야 합니다.
Thrust = Drag + Weight×sinθ
∴ sinθ = (Thrust -Drag)/Weight = 잉여추력/Weight
따라서 상승각(θ)은 순수하게 추력과 항력(또는 잉여추력), 그리고 중량에 영향을 받는다는 사실을 알 수 있습니다. 만약 잉여추력이 0이 되면 θ도 0이 되어 직진수평비행 상태가 되고, 잉여추력이 중량과 같다면 θ는 90가 되어 수직상승을 할 수 있게 됩니다.
이번에는, 상승 중 비행기에 작용하는 모든 힘들을 '수평으로 작용하는 힘'과 '수직으로 작용하는 힘'으로 나눠서 살펴 봅시다.

θ가 0이 아닐 때(상승비행을 할 때),
수평으로 작용하는 힘의 총 합: Thrust×cosθ - (Lift×sinθ + Drag×cosθ) = 0,
(Thrust - Drag)×cosθ = (잉여추력)×cosθ = Lift×sinθ
수직으로 작용하는 힘의 총 합: Thrust×sinθ + Lift×cosθ - (Drag×sinθ + Weight) = 0,
(Thrust - Drag)×sinθ + Lift×cosθ = (잉여추력)×sinθ + Lift×cosθ = Weight
여기서 중요하게 봐야할 것은 바로 '양력'입니다.
비행기가 수평비행을 할 때는 양력의 크기와 중력의 크기가 서로 같지만,
θ가 0일 때(수평비행을 할 때), cosθ는 1, sinθ는 0이기 때문에,
수평으로 작용하는 힘의 총 합: Thrust - Drag = 0 (잉여추력 0)
수직으로 작용하는 힘의 총 합: Lift - Weight = 0
상승비행을 할 때는 추력의 수직분력에 의해 오히려 수평비행 때보다 양력이 상대적으로 작아져야 한다는 것을 알 수 있습니다.
수직으로 작용하는 힘의 총합: (잉여추력)×sinθ + Lift×cosθ = Weight
여기서 잉여추력(Thrust - Drag)의 크기는 Weight×sinθ(항력의 방향으로 작용하는 중력의 성분) 이므로,
Lift×cosθ = Weight - Weight×sin²θ = Weight×(1 - sin²θ) = Weight×cos²θ,
∴ Lift = Weight×cosθ
따라서 양력은 상승각(0~90도)이 커질수록 작아짐.
따라서 엄밀한 의미에서 비행기가 직진수평 비행 때와 동일한 속도로 상승하려면 받음각(AOA)을 줄여줘야 합니다.
그러므로 기본적으로는 속도가 일정하다고 가정할 때 상승각도에 따라서 수평비행을 할 때보다 조종간을 더 눌러주거나 down trim을 더 사용해야 합니다.
When the airplane is in steady flight with moderate angle of climb, the vertical component of lift is very nearly the same as the actual lift. Such climbing flight would exist with the lift very nearly equal to the weight. (인용출처: AERODYNAMICS FOR NAVAL AVIATORS(H. H. Hurt, Jr.), p152)
하지만, 상승각도가 크지 않을 때는 어느정도 무시할 수 있는 부분이므로 통상 상승시 양력은 직진수평비행을 할 때와 같다고 보기도 합니다.
실제로도 동일한 속도에서 상승비행 중 trim과 수평비행 중 trim이 크게 차이가 나지는 않습니다. 또한 어떤 비행기들은 세로안정성을 위한 설계가 반영되어 추력이 증가하면 기수가 저절로 떨어지기 때문에 오히려 조종간을 더 당겨주거나 up trim을 사용해야 할 수도 있습니다.(그래서 DA40가?)


비행기의 강하(Descent)
직진수평비행에서 강하비행으로 전환하기 위해서는 먼저 양력을 감소시켜야 합니다. 중력보다 작은 양력은 항공기를 아래로 가속시키게 되며 직진경로를 강하경로로 변화시키게 됩니다.

상승비행과 마찬가지로, 이렇게 일단 원하는 강하경로로 진입하고 나서는 다시 힘의 평형을 유지해야 일정한 각도로 계속 강하할 수 있습니다.

이 때 중력(Weight)은 상승비행을 할 때와 반대로 추력(Thrust)을 보조하는 쪽으로 작용하기 때문에, 추력을 줄이지 않으면 비행기는 수평비행을 할 때 보다 속도가 증가하게 됩니다. 또한 항력(Drag)은 양력을 보조하는 방향으로 작용하기 때문에 강하비행을 유지하기위한 양력의 크기는 수평비행을 할 때보다 작아지게 됩니다. 그리고 아주 극단적인 수직강하의 경우 양력은 0가 되어야 합니다.

그리고 이 때는 추력이 0되어도 순수하게 중력만으로 강하할 수 있는데, 이렇게 되면 사실상 비행기는 자유낙하를 하는것이 됩니다. 참고로 이렇게 자유낙하를 하더라도 계속해서 항력이 증가하기 때문에 비행기는 결국 힘의 평형을 이루고 일정한 속도로 강하하게 되는데, 이 일정한 속도를 '종단속도(Terminal velocity)'라고 합니다.
이와 같이 비행기가 직진수평 비행 때와 동일한 속도로 강하려면 상승비행을 할 때와 마찬가지로 받음각(AOA)을 줄여줘야 합니다. 하지만 강하각이 크지 않을 때는 직진수평비행을 할 때와 양력의 차이가 거의 나지 않고 비행기 각각의 고유한 특성 때문에, 실제로는 강하비행에 사용되는 trim과 수평비행에 사용되는 trim에는 큰 차이가 없습니다.
'비행기 조종사 학과 > 비행원리' 카테고리의 다른 글
| 실속(Stall)과 하중계수(Load factor) (16) | 2021.04.07 |
|---|---|
| 하중계수(Load Factors) (11) | 2021.03.22 |
| 비행기동에서의 공력학적 힘 (선회) - 1 (37) | 2021.02.23 |
| Free Directional Oscillations(Dutch Roll) 과 Spiral Instability (6) | 2021.02.10 |
| 방향(수직)안정성 (Directional(Vertical) Stability) (17) | 2020.11.13 |





