| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Best Glide Speed
- 2007년 제3차 운송용조종사 변형
- icao
- FPNM
- sideslip
- 항공안전법
- Turn radius
- 2007년 제4차 자가용조종사 변형
- dutch roll
- Propeller
- load factor
- ICAO Annex 14
- 국제민간항공협약
- UAM
- 13년도 공단 기출문제 변형
- annex14
- dihedral effect
- Lead Radial
- Today
- Total
비행사의 다이어리
THE AVIATION CALCULATION: VVI(VSI) 계산법의 적용 본문
THE AVIATION CALCULATION
VVI(VSI)값 정하기(계속)
이번에는 IAP 차트에서 VVI값 구하기가 어떻게 적용되는지 알아보자~.
먼저 무안공항(RKJB) RWY01 VOR Approach Chart를 보자.

VOR은 Radial 같은 수평유도 정보만을 제공하기 때문에 VOR 수신기를 통해서 가고자 하는 항로로부터 얼마나 벗어낫는지는 바로 바로 확인이 가능하다. 반면 수직유도 정보는 제공하기 않기때문에 VOR 접근과 같은 비정밀접근에서 수직항법(소위, Vertical NAVigation)은 고도계와 거리를 측정하는 DME기기등을 확인한 후 조종사가 머리속으로 수직방향으로 비행이 어떻게 되가고 있는지 해석하는 방식으로 이루어진다. 따라서 차트를 보고 각 step down point 간 고도를 처리할 수 있는 VVI값을 계획하는것은 착륙의 성공을 위해 매우 중요하다. 특히 MDA 도달 이후 활주로가 시야에 들어왔을때 마지막으로 강하 해야 하는 시점을 결정해야 하는데, 안정적으로 강하를 시작할 수 있는 적절한 point, 즉 적절한 VDP(Visual Descent Point)를 결정해야 고도가 모자르지도 많지도 않게 좋은 강하율로 활주로에 도달 할 수있다.
장애물 회피 등 목적으로 VDP는 "V" 형태로 차트에 표기되기도 하지만 위 무안 VOR 접근 차트를 보더라도 알 수 있듯이 대부분 우리나라 공항의 비정밀접근 차트는 VDP가 명시되어있지 않다. 따라서 제일먼저 VDP를 설정 하는 것 부터 짚어 보겠다.

3도 강하각을 기준으로 하였을때 60 대 1 법칙에 의하여 강하율은 300FPNM이 된다. 이제 활주로에서 MDA까지 높이(FT)를 구하고, 구한 높이에 300FPNM을 나누어 주면 위 그림처럼 활주로로 부터 강하시점까지의 거리, 즉 VDP를 구할 수 있다.
(MDA - RWT ELEV) ÷ Gradient(통상300FPNM)
만약 HAT(Height Above Touchdown)과 같은 정보가 차트에 나와있다면 MDA에서 활주로 고도를 빼는 번거로움을 줄일 수 있다.
HAT ÷ Gradient
이제 다시 무안공항 차트를 보자. 차트에 나와있는 MDA는 910FT, 활주로 고도는 32FT, 그러므로 활주로에서 MDA까지 높이는,
910 - 32 = 878FT
3도 강하각으로 내려간다고 가정할때,
878 ÷ 300 ≒ 2.9NM
따라서 VDP는 활주로로 부터 2.9NM 떨어진 지점이 되겠다. 활주로를 기준으로 일단 VDP를 구하였지만 우리는 VOR DME로 부터 거리정보를 얻기때문에 NM을 DME로 보정 해 주어야 한다. 다시 차트로 돌아가 FAF 위치를 찾아보자.

FAF는 활주로로 부터 5NM 떨어져있고 이때 DME가 4.5가 됨을 알 수 있다. 즉, 활주로로 부터 실제거리와 무안 VOR(MUN) DME간에 0.5만큼 차이가 존재한다. 따라서 2.9NM을 0.5만큼 빼서 DME로 바꾸어 주면 2.4DME가 나온다.
따라서 위 차트의 VDP는 무안 VOR(MUN) DME 기준으로 2.4DME로 정할 수 있다.
그리고 VVI값은 VDP를 3도 경사각, 즉 300FPNM 강하율로 설정하였기 때문에, 이때 접근 속도가 70KTAS라면, 앞 포스팅에서 질리도록(?) 살펴보았듯이 350FPM이 나온다.
(70 ÷ 60) × 300 = 350FPM

참고로 활주로 주변에 PAPI와 같은 진입각지시등이 있다면 진입각지시등이 정상접근을 가리키는 위치가 바로 VDP이다. 실제 비행할때 계산된 VDP와 비교해 보는것도 재미있을 듯..
VDP부터 VVI 값까지 구했다고 계기만 보고 활주로로 접근하면 절대 안된다. VDP이후로는 반드시 활주로를 시야에 두고 MDA이하로 강하해야한다. 그때 부터는 시계접근이다. 내려가면서 혹시라도 있을지 모를 장애물을 눈으로 보고 피해가야한다. 우리가 구한것은 잘 내려가기 위한 하나의 계기 참조점일 뿐이다. 특히 차트에 VDP가 표시되어있지 않을때 정말 주의해야한다. VDP가 차트에 표기되지 않은데에는 여러가지 이유가 있겠지만 장애물 유무와 관계없이 VDP를 계기접근 절차에 의무적으로 포함해야할 사항이 아니라서 그냥 차트에 표기를 안한 경우도 있다고 한다. 다시한번 강조하지만 MDA도달 후 강하를 결정하는것은 바로 조종사 자신이다. 계산된 VDP와 VVI값이 아니다!.

자, 그 다음엔 같은방식으로 무안 VOR 접근차트에서 FAF 고도에서 VDP MDA까지 지속적으로 강하하기 위해서 얼마만큼의 PITCH변화와 VVI값이 필요한지 알아보자.
먼저 FAF부터 VDP까지 거리를 구해보자.
FAF = 4.5DME, VDP = 2.4DME 이므로,
FAF 부터 VDP까지 강하거리는,
4.5 - 2.4 = 2.1NM 이다.
그리고 FAF부터 VDP까지 고도차이를 구하자.
FAF = 1700FT, VDP = MDA = 910FT 이므로,
FAF에서 VDP까지 내려갈때 고도 변화는,
1700 - 910 = 790FT 이다.
따라서 FAF부터 VDP까지 거리에 따른 고도변화율, 즉 강하율(Descent Gradient)은,
790FT / 2.1NM ≒ 376FT/NM, 즉 376FPNM이 된다.
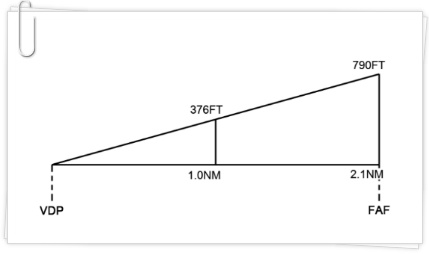
이때 접근속도를 70KTAS로 가정하고, 376FPNM 강하율을 맞추기 위해서
PITCH는 70KTAS 수평비행 PITCH 보다 3.76도 낮은 PITCH를 유지하고(60 대 1의 법칙),
VVI값은 대략 440FPM이 나온다(항법계산).
이와같은 계산을통해 FAF에서 70KTAS로 VVI 440FPM으로 맞추어 내려가면 깔끔하게 VDP에 도달함과 동시에 MDA에 도달할 수 있다.
그리고 동일한 방법으로 이어지는 step down에도 적용하여 똑같이 최적 강하율과 VVI 값을 구할 수 있다.
지금까지 무안공항(RKJB) RWY01 VOR Approach Chart에서 항법계산으로 구해본 내용들을 종합적으로 정리해 보면,
70KTAS로 접근한다고 가정할때, FAF부터 VDP까지 440FPM으로 강하하면 3.76도 강하각으로 고도 790FT가 처리되며,
그 이후로 VDP부터 활주로까지 350FPM으로 강하하면 3도 강하각으로 878FT가 처리되어 활주로 까지 도달 할 수 있다.
이와같은 방법으로 계획을 세우면 각 step down에서 수평비행 없이 흡사 정밀접근처럼 끊김없는 강하가 가능하다. 하지만 사실 기동성이 좋은 소형항공기의 경우 VDP까지 연속적으로 내려가기 보다는 최대한 빨리 MDA까지 내려가 MDA고도에서 수평비행을 통해 공항을 찾는것이 훨신 착륙에 유리하다. 다만 위 계산을 하는 이유는 큰 항공기의 경우 기동성이 떨어지기 때문에 비정밀 접근시 중간중간 수평비행을 동반한 계단식(step down)비행보다는 정밀 접근과 비슷한 형태로 비행하는것이 자세변화를 줄여 안정적인 접근을 하는데 도움이 되기 때문이다. 그러니깐 연속된 부드러운 접근이 꼭 좋은것만은 아니라는 것이다.

역시 동일한 방법으로 정밀접근을 수행할때 VVI값을 계산할 수 있다.
정밀접근이야 뭐 ILS 수신기에 Glide Slope(GS) 정보가 시현되기 때문에 적절히 강하율을 조절하여 GS Indicator를 잘 물고 내려가기만 하면 된다. 이때 VVI값을 계산 해 두면 Glide Slope에 따라 적절히 강하율을 조절 할 때 좋은 참조점으로 삼을 수 있다. 만약 실제로 GSI를 따라 정밀접근을 하고 있을때 계산한 VVI값과 실제 VVI값이 차이가 많이 난다면 현재 항공기에 어떤 외력(가령 바람이라든지)이 작용하고 있다던지 더 넓게는 계기에 어떤 문제가 있을수 있다던지 등을 알 수가 있다. 이와같이 정밀접근에서 VVI값을 미리 계산을 해두면 접근에 방해가 되는 요소들을 생각하고 식별할 수 있어서 실패접근(Missed Approach) 수행여부를 판단하는데에도 참고 할 수 있다.
한번 실제로 무안공항(RKJB) ILS Y RWY01 Approach 차트에서 FAF 이후 Glide Slope을 따라 몇 FPM으로 내려가야할 지 계산해 보자.
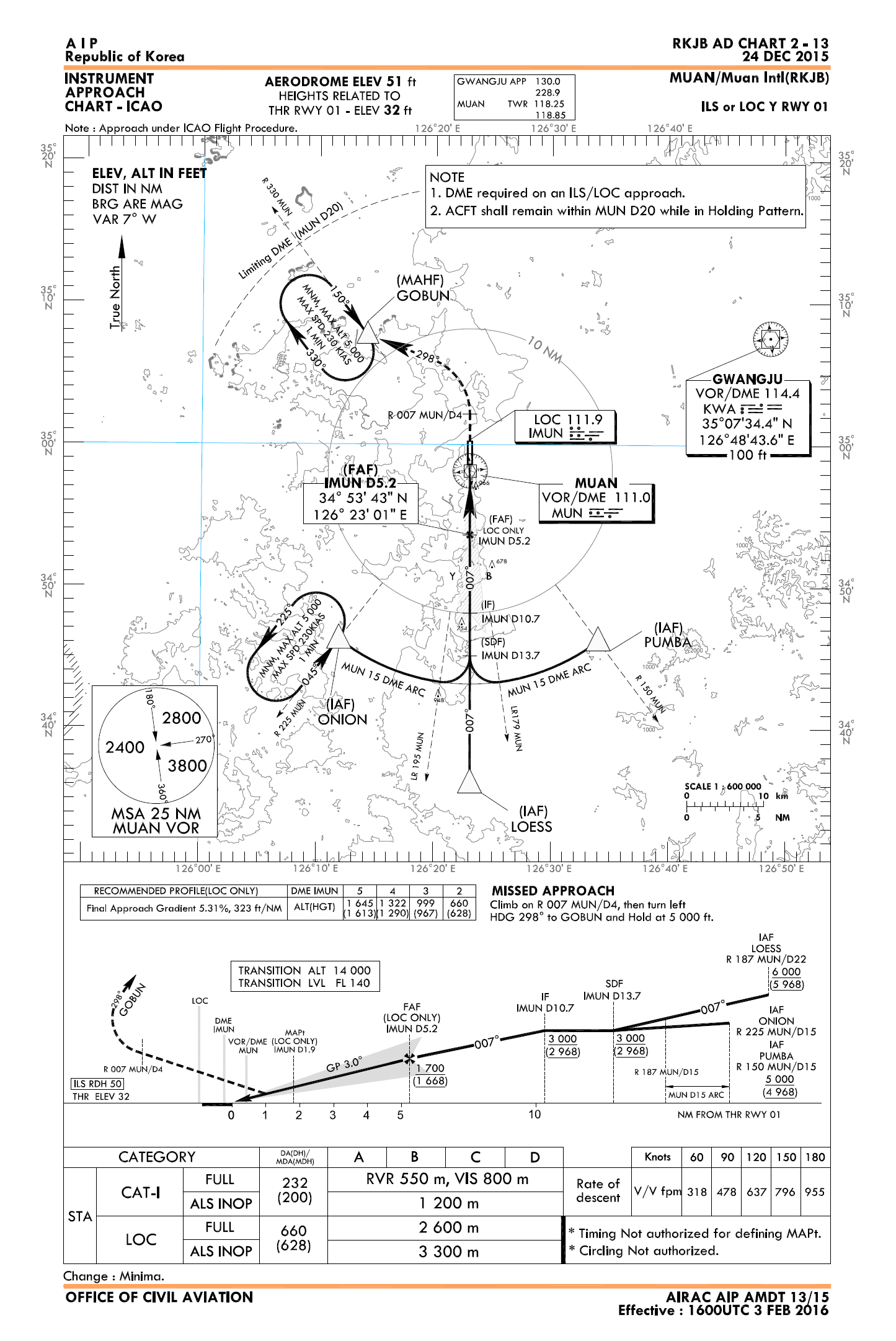
Glide Slope이 3도로 설정되어 있음으로 300FPNM,
여기서 VVI값(FPM)을 구하기 위해 접근속도를 70KTAS로 설정하면,
앞서 여러번 구했던 방식으로 350FPM이 나온다.
따라서 70KTAS로 Glide Slope 물때 VVI를 350FPM으로 유지하면 흐트러짐 없이 Glide Slope을 물고 내려갈 수 있겠다.
보다시피 정밀접근은 VDP, step down같은 요소들이 별로 없어 VVI 값 계산이 매우 단순하다.
그래서 기왕 하는김에 Glide Slope을 물기 전 IF 부터 FAF 까지 90KTAS로 접근했을때 VVI 값도 구해보았다.
(step down 계산방법과 동일)
IF에서 고도가 3000FT, FAF에서 고도가 1700FT 이므로,
IF에서 FAF까지 처리해야 할 고도는 3000 - 1700 = 1300FT
IF위치는 10.7DME, FAF의 위치는 5.2DME 이므로,
IF에서 FAF까지 거리는 10.7 - 5.2 = 5.5NM
따라서 Descent Gradient 는 1300/5.5 ≒ 236FPNM
그러므로 (90/60) × 236 = 354FPM, VVI 값은 354FPM이 나온다.
정리하면 이렇다. IF에서 90TKAS로 VVI 354FPM을 유지하여 FAF까지 강하하고, FAF에서 70KTAS로 속도를 줄인 후에 Glide Slope을 물고 VVI 350FPM으로 활주로로 접근하여 착륙한다.
참고적으로 3도 강하각과 2.5도 강하각의 경우 간단하게 VVI값을 구하는 공식이 있다.
3도 강하각에 대한 공식은 : TAS × 10 ÷ 2
2.5도 강하각에 대한 공식은 : (TAS × 10 ÷ 2) - 100
위에서 했던 계산을 이 공식에 대입해서 다시 적용해 보면
70KTAS, 3도 (Glide Slope) : 70 × 10 ÷ 2 = 350FPM
90KTAS, 2.5도 (정확히는 2.36도 지만 편의상 2.5도로 보자) : (90 × 10 ÷ 2) - 100 = 350FPM
비슷하게 나오는것을 볼 수 있다.
급하게 FPM을 구해야 할 경우 참조하면 좋을것이다.

지금까지 강하비행과 관련된 VVI값을 구하는 항법계산들을 쭉 정리 해 보았다. VVI값을 구하기위한 속도를 "진 대기속도(TAS)"로 설정 하였는데 좀 더 정밀한 계산값을 얻으려면 TAS 대신 수평면 위를 실제로 나아가는 속도인 "대지속도(Ground speed)"를 사용하면된다.
'VVI(VSI)값 정하기' 내용은 여기에서 마무리 지을까 한다. 다음 포스팅 부터는 선회반경과 관련된 항법계산들을 쭉 정리해 보고자 한다. 교관님께서 알려주신 Lead Radial 구하는 공식이 과연 어떤 원리로 튀어나온것인지, 이제부터 본격적으로 파헤쳐 볼것이다.

GOOD DAY~ ;)
참고문헌 : AFM11-217V3
'계기비행 규칙(IFR) > 60대 1의 법칙과 항법계산' 카테고리의 다른 글
| THE AVIATION CALCULATION: DME arc 관련 계산식 (14) | 2020.07.08 |
|---|---|
| THE AVIATION CALCULATION: 선회반경(선회 반지름)의 계산 (4) | 2020.07.08 |
| THE AVIATION CALCULATION: VVI(VSI)의 결정 (0) | 2020.07.08 |
| THE 60-TO-1 RULE(60 대 1의 법칙) (0) | 2020.07.08 |




