| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Turn radius
- dutch roll
- 2007년 제4차 자가용조종사 변형
- 항공안전법
- 국제민간항공협약
- UAM
- ICAO Annex 14
- 13년도 공단 기출문제 변형
- icao
- 2007년 제3차 운송용조종사 변형
- Best Glide Speed
- FPNM
- load factor
- sideslip
- dihedral effect
- Lead Radial
- annex14
- Propeller
- Today
- Total
비행사의 다이어리
THE 60-TO-1 RULE(60 대 1의 법칙) 본문

무안에서 계기 훈련 비행을 할때의 일이다.
계기접근을 위하여 IAF onION에서 15 DME ARC TURN을 그리고 있을때, 당시 교관님께서 'ARC에서 최종접근경로(Final Approach course)를 타기위해선 Lead Radial을 몇으로 잡을 것인가'에 대해 물어보셨다.

차트상에는 위 그림처럼 195 Radial을 Lead Radial(LR)으로 잡았다. 즉 최종접근경로 007도 에 해당하는 187 Radial 의 8 Radial 전을 LR로 잡은것인데 문제는 저 값이 접근속도가 빠른 대형항공기를 위한 값이지 우리처럼 작은 자가용 항공기를 위한 값이 아니라는데에 있다. 따라서 우리는 통상 4 Radial 전인 191 Radial을 LR로 잡는다. 이유는 모른다. 왜 4 Radial인지. 그때 당시에는 다른 교관님들도 LR을 4 Radial로 잡으라고 하니 그냥 경험상 '그 쯤' 해서 돌면 자연스럽게 최종접근경로를 탈수 있어서 정해진 줄 알았다.
나는 교관님께 자신있게 4 Radial 전인 191 Radial을 LR로 잡는다고 말했다. 그러자 교관님은 '왜 그렇게 잡았는지'를 물으셨는데, 역시 자신있게 '실제로 해본 경험상 그 쯤에 적절해서 잡았다'고 말했다. '그럼 실제로 비행해보지 않은 공항에서는 어떻게 차트를 보고 접근 계획을 세울것인지' 교관님이 다시 내게 묻자. 나는 '적절히...' 말을 잇지 못했다. 그렇다. LR을 잡는 참조할 만한 기준이 없었던 것이다.
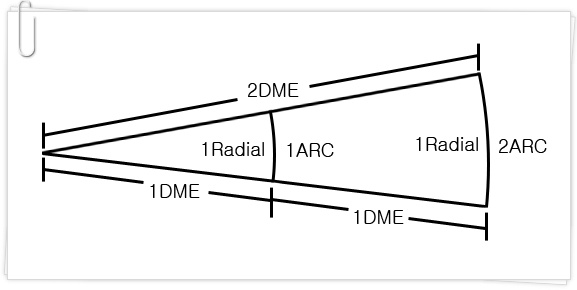
원의 반지름이 커지면 1도에 해당하는 원주 호의 길이가 길어지듯이,
DME ARC라는 것도 DME 거리에 따라서 1 Radial에 해당하는 경로의 거리가 달라진다.
따라서 속도가 일정하다고 가정해도 DME 거리가 달라지면 LR이 항상 4 Radial일 수 없었기에 나는 말문이 막힐 수 밖에 없었다.

하...
대답못하는 나를 위해 교관님은 60을 DME로 나누고 진대기속도(TAS)의 1%를 곱해서 LR이 4 Radial이 됨을 설명해 주었다.
수식으로 나타내면, LR=(60/DME)×(1×TAS/100)
즉, 무안 RWY 01 IAP, DME ARC의 DME는 15, 이때 TAS를 100kts로 가정할때,
(60/15)×(1×100/100)=4=LR 이 된다.
비행을 마치고 나서 나는 이 계산식이 어떻게 나온것인지 궁금해졌다.
DME, 속도 그리고 선회반경(Turn Radius;TR)과 연관이 있을듯 보였다.
나는 계기비행과 관련된 계산식들이 정리된 책들을 뒤지다가 "AIR FORCE MANUAL 11-217, VOLUME 3 SUPPLEMENTAL FLIGHT INFORMATION"이라는 책에서(더 정확히는 Chapter 3) 해당 공식과 관련된 광범위한 계산식들을 찾을 수 있었다.
THE 60-TO-1 RULE(60 대 1의 법칙)
모든 항법 계산의 기초가 되는 법칙이다. 간단히 설명하면 60NM 떨어진 곳에서 1도의 크기는 1NM에 해당한다는 법칙이다. 아래 그림을 보면 이해가 빠를듯.

이 법칙에 따라,
1. 60NM 떨어진 ARC 호의 1 Radial에 해당하는 길이는 1NM이 되거나,
항로에서 1도 벌어졌을때 60NM을 가면 항로로 부터 1NM 벗어나게 됨을 알 수 있으며,
2. 상승각 또는 강하각을 1도 바꾸어 60NM을 비행하였을때 고도는 1NM 상승 또는 강하됨을 유추할 수 있다.
여기서 우리는 보통 고도는 FT 단위를 씀으로 1NM을 FT로 바꾸면 약 6076FT, 즉 6000FT에 근사 시킬 수 있다.
1NM≒6000FT, 그러므로 자세를 1도 바꾸어 60NM을 비행하였을때 고도는 6000FT 변화가 생긴다고 볼 수 있다.
그렇다면 어떻게 1도에 해당하는 거리가 60NM에서 1NM이 될까?
이 궁금증을 해결하기 위해 중/고등학교 수학문제로 돌아가보았다.
코사인 제2법칙... 이과 학생들이라면 낯설지 않은 단어이겠다. 나는 이 문제를 풀기 위해 이등변 삼각형에 근사 시켜 보았다.

방법은 간단하다. 위 삼각형에서 'a'변과 'b'변이 같은 이등변 삼각형이라고 가정하고,
'a'와 'b'에 60NM을 대입, a=b=60NM
'θ'는 1도를 대입, θ=1˚
그리고 코사인 제2법칙으로 계산하여 'c' 값이 얼마가 나오는지 확인해 보는 것이다.
자 이제 공학용 계산기를 뚜드려 보면.... .. ... . ...

c=1.09659486NM, 대략 1NM정도가 나오는것을 확인할 수 있었다.
탄젠트...(2016.03.23 내용 추가) 그리고 더 간단한 방법이 있었다. 바로 탄젠트 계산법.

'b'에 60NM을 대입하고, b=60NM
'θ'에는 1도를 대입하여, θ=1˚
위 그림에 나와있는 탄젠트 계산식으로 'a' 값을 구해보면
a=1.047303896NM
간단하게 1NM에 근사함을 확인할 수 있다.
부채꼴 호의 길이... 위 AFM11-217 에서도 나와있는 방법, 이번에는 이 방법으로 접근해 보겠다.
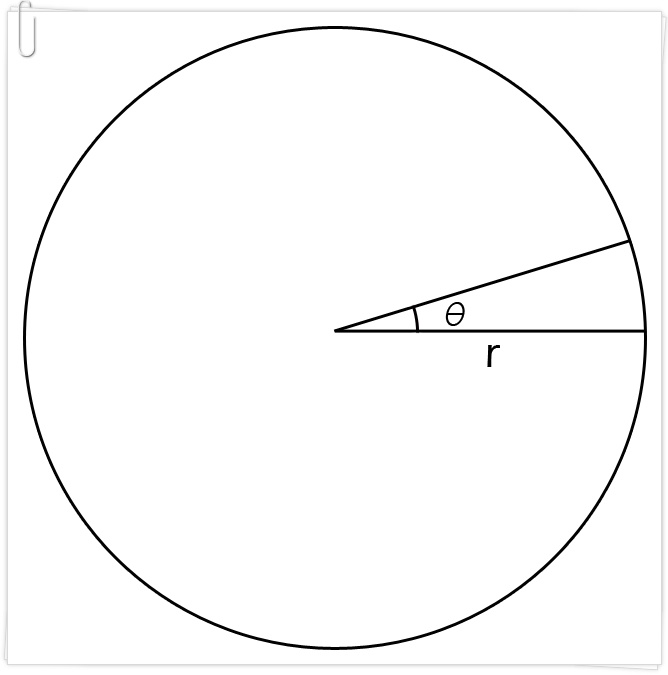
중학교 지식을 상기해보면 원주의 길이는 2πr,
여기서 π=3.14(설마 이것을 모르는 사람은 없겠지??)
따라서 반지름r이 60NM인 원의 원주 길이는
2×3.14×60=376.8NM
여기서 해당 원의 360도 중1도에 해당하는 부채꼴의 호의 길이는 전체 원주의 1/360 이므로
376.8×1/360=1.046666667NM, 역시 대략 1NM이 나오는것을 확인할 수 있다.
사실 이론적으로 완벽하게 1도 부채꼴의 호의 길이가 1NM가 되는 반지름을 구해보면,
2πr × 1/360 = 1,
r = 360/2π = 57.295779513082320876798154814105...
180/π, 대략 57.3NM이 나온다. 하지만 계산상의 편의를 위해 π값을 대충 3으로 잡고 60NM로 퉁치는 것이다. 1NM이 6,076.1154855643044619422572178478FT이지만 그냥 6,000FT로 퉁치것과 비슷한 이치다. <2021. 7. 19 내용 추가>
이제 증명이 되었으니 응용을 해보자.
위 법칙이 선형적으로 비례됨을 가정할때, 60NM 떨어진 곳에서 2도의 크기는 2NM이 될것이고, 30NM 떨어진 곳에서는 1NM이 될것이다.
즉, (당연한 이야기 이지만) 각도 크기에 해당하는 거리는 각도와 거리에 비례함을 알 수 있다.

다만 이 법칙을 적용할 때 위 그림에서 처럼 각도가 커지면 오차가 커지기 때문에 큰 각도로 계산하여 적용할때는 특별히 주의 해야 할 것 같다.
여기서 문제!, 만약 항로에서 3도 벗어난 채로 40NM을 비행하였다면 원래항로부터 몇 NM 이상 떨어져 있을까?

<문제의 답에대한 대단히 정직한 짤>
그러하다...... 어째든;;, 이정도 문제를 풀수 있으면 수평방향에 적용하는데는 큰 문제가 없을것이다.
그렇다면 이번엔 수직방향으로도 적용하면?
항공기 자세를 2도 변화시켜 60NM을 비행하면 2NM의 고도 변화, 즉 12000FT의 고도변화가 생길것이고(1NM≒6000FT), 30NM 비행하면 마찬가지로 6000FT의 고도변화가 생길것이다.
결국 앞서 설명한 내용과 결국 똑같은 내용이다. NM을 우리가 사용하기 쉽게 FT로 바꾸었을 뿐,
그럼 여기서 좀더 나아가서, 똑같은 조건에서 비행거리만 다르게 1NM을 비행했다고 가정하면 어떻게 될까?
12000FT/60NM, 또는 6000FT/30NM 해보면,
정답은 200FT, 즉, 200FT/NM이다. Clime Gradient 상승 경사율 단위인 FT/NM(FPNM)가 튀어 나왔다.

그러므로 200FPNM을 유지하려면 2도 상승각으로 비행해야함을 알수있다.
이번엔 상승 경사율 100FPNM을 유지하려면 몇도 상승각이 필요한지 알아보자.
100FPNM으로 60NM비행하면, 100FPNM×60NM, 즉 6000FT 고도상승이 이루어지므로 60대 1의 법칙에 의거하여 1도 상승각으로 비행하고 있음을 알 수 있다.
마찬가지로 방법으로 3도 상승각으로 비행하면 300FPNM 상승 경사율을 얻을것이고, 강하각의 경우도 동일한 결과를 얻을 수 있다.
대표적으로 우리가 흔히 활주로에 접근할 때 3도 강하각으로 접근하는데 이는 300FPNM의 강하 경사율이 적용되는것을 알수 있다.
따라서 각도와 상승/강하 경사율(FPNM)은 선형적으로 비례한다고 볼 수 있으므로 우리는 자세계 PITCH 변화각만을 토대로 몇 FPNM 상승 또는 강하하고 있는지 알 수가 있다.

가령 속도의 변화가 없음을 가정하고 수평비행시 자세계가 상승 PITCH 1도를 가리키고 있을때 200FPNM으로 상승하고자 한다면 현재 자세계가 가리키고 있는 1도에서 2도를 더한 3도 상승 PITCH각을 유지하면 될 것이다. 300FPNM으로 강하하고자 할때도 마찬가지로 수평비행 상태에서 현 자세계가 가리키고 있는 1도에서 3도를 뺀 -2도, 즉 2도 강하 PITCH각을 유지해야 할 것으로 생각할 수 있다.



위 예시에서 "속도의 변화가 없음"을 가정하였는데, 이는 상승이나 강하시에도 AOA(Angle Of Attack;받음각)변동이 없음을 가정한 것이다. 그러므로 실전에 적용할때는 속도의 변화에 주의해야 하며 속도가 많이 변하는 상승 보다는 강하할때 적용하는것이 좋을 것 같다.
다만, 이것 역시 각도가 커지면 계산 오차도 커지기 때문에 PITCH 변화각이 클때는 유의해야 한다.
(물론 그전에 속도 변화가 심하여 AOA변화가 커지기 때문에 신뢰할 수 없을 것이다.)
60 대 1 의 법칙(60 to 1 Rule)은 여기까지.
다음 포스팅에서는 오늘 살펴본 내용을 근간으로 다양하게 파생되는 항법계산(Aviation calculation)들을 정리해 보겠다.
(아직 LR 정리 까지 갈려면 갈길이 너무너무 멀다....;;)
Good day~
참고문헌 : AFM11-217V3
'계기비행 규칙(IFR) > 60대 1의 법칙과 항법계산' 카테고리의 다른 글
| THE AVIATION CALCULATION: DME arc 관련 계산식 (14) | 2020.07.08 |
|---|---|
| THE AVIATION CALCULATION: 선회반경(선회 반지름)의 계산 (4) | 2020.07.08 |
| THE AVIATION CALCULATION: VVI(VSI) 계산법의 적용 (2) | 2020.07.08 |
| THE AVIATION CALCULATION: VVI(VSI)의 결정 (0) | 2020.07.08 |




