| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- dutch roll
- Lead Radial
- ICAO Annex 14
- UAM
- annex14
- Propeller
- 2007년 제4차 자가용조종사 변형
- FPNM
- sideslip
- 국제민간항공협약
- load factor
- 13년도 공단 기출문제 변형
- Turn radius
- dihedral effect
- icao
- 2007년 제3차 운송용조종사 변형
- Best Glide Speed
- 항공안전법
- Today
- Total
비행사의 다이어리
THE AVIATION CALCULATION: 선회반경(선회 반지름)의 계산 본문
THE AVIATION CALCULATION
선회반경(또는 선회 반지름; Turn Radius; TR)의 계산
비행기의 모든 운동은 양력과 연관 되어 있다. 그리고 대부분의 양력은 비행기에서 제일 커다란 주 날개에서 만들어 진다. 따라서 주 날개를 비스듬하게 기울이면(Bank) 양력의 방향이 비스듬히 기울어 진다. 사이드슬립이 없다는 가정하에 양력이 비스듬히 기울어져 발생하면 비행기는 비행방향이 계속 바뀌게 된다.

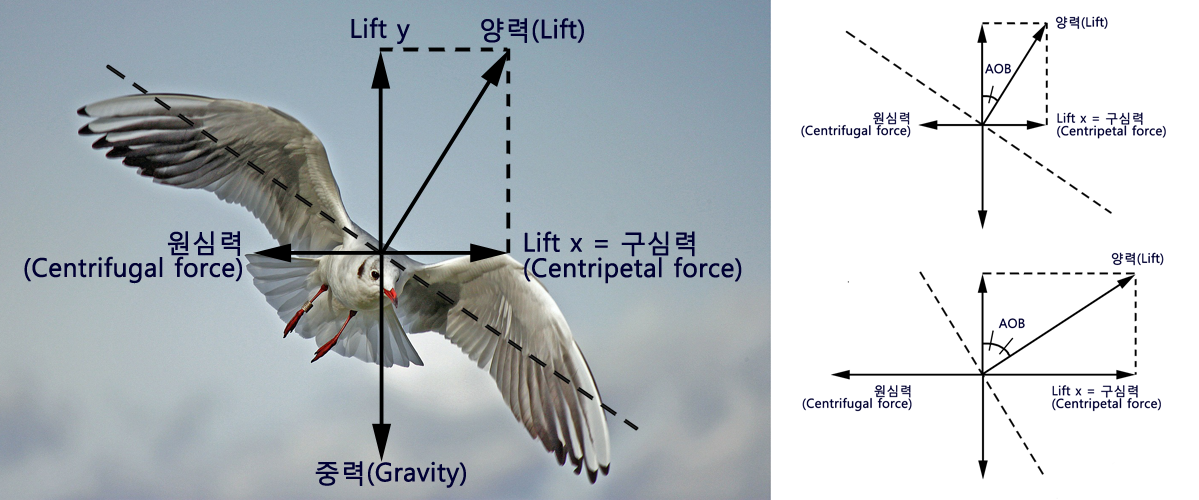
즉, 비행 중 선회는 날개의 기울어진 정도(Angle Of Bank; AOB)에 영향을 받으며 이 때 발생한 양력의 수평성분은 선회의 원동력인 '구심력'을 제공한다. 위 그림처럼 수평비행 상태에서 날개에 AOB를 많이 주게 되면 '중력'에 대항하여 양력의 수직성분(Lift y)을 유지시키기 위해 양력(Lift)를 증가시켜야 되는데, 이때 양력의 수평성분(Lift x)이 자연스럽게 같이 증가되므로 '구심력'이 증가하게 된다.
특정 AOB에서 양력(Lift)에 대한 양력의 수평성분(Lift x) 값은 다음과 같이 나타낼 수 있다.


여기에다 '수평 비행 상태', 즉 'Lift y = 중력(=질량×중력가속도)' 조건을 식으로 나타내면,
여기서 m은 비행체의 질량, g는 중력가속도를 나타낸다. 위 식을 정리하면 비행체의 무게와 AOB를 알면 양력을 구하는 식을 구할 수 있는데,
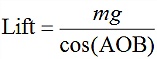
이 양력(Lift)을 구하는 식을 Lift x 식에 대입하면,

Lift x, 즉, 구심력은 중력(mg)의 탄젠트 AOB 값이 됨을 알수 있다.
따라서, 수평비행 상태에서 AOB가 커지면 구심력(Lift x)도 같이 커지며, 90도에서는 무한대 값이 된다.
한편 속력은 '원심력'을 제공한다. 따라서 속력이 증가하면 원심력이 증가하게 되는데 이를 나타내는 대표적인 공식은 다음과 같다.

여기서 V는 비행체의 속력, r은 선회반경(반지름)이다.
그리고 비행체가 선회반경이 일정한 등속 원운동을 하기 위해서는 '구심력'과 '원심력'이 같아야 함으로, 구심력(Lift x ) = 원심력 이어야 한다.

위 식을 정리해서 선회반경 r을 구해보면,

최종적으로 위 식과 같이 됨을 알 수 있다.
따라서 수평비행 상태에서는, AOB가 일정한 상태에서 속도가 증가하면 '원심력'이 증가하여 선회반경이 커지고, 속도가 일정한 상태에서 AOB가 증가하면 '구심력'이 증가하므로 선회반경이 작아지는 것이다. 아울러 선회반경을 결정하는 변수가 속도 V와 AOB 이 두 가지 뿐임으로 비행체의 종류, 무게, 크기, 형상등은 선회반경이 결정되는데 영향이 거의 없음을 알 수 있는데, 이와같은 특징으로 'General Turning Performance (GTP)차트'가 만들어 질 수 있다.

그런데 여기서, 잠깐! AOB가 일정할때 속도가 증가하면 양력도 증가하기 때문에 '구심력'도 같이 커지니깐 선회반경이 반드시 커지는 것은 아니지 않냐고 생각할 수 있지 않을까?
어떻게 생각하는가?
.
.
.
정답은 '절대 그런일은 일어나지 않는다'이다. 왜냐하면 '수평비행'상태라는 조건이 붙기 때문이다. AOB가 일정한 상태에서 속도가 증가하여 양력이 증가하면 양력의 수직 성분(Lift y)도 같이 커져 상승선회를 하게 되기 때문에 수평비행을 유지하려면 속도에 따른 양력의 증가분 만큼 의도적으로 받음각(AOA)을 줄여 양력계수 CL값을 낮춰 주어야 한다. 따라서 양력은 항상 일정하게 유지되므로 '구심력'도 일정하게 유지가 된다.
이제 관련된 예제들을 한 번 풀어보자.
> 무풍상태의 공간에서 비행기가 30도 Bank, 100KTAS로 수평 선회할때 선회반경(TR)은 어떻게 될까?

일반적으로 우리는 중력가속도g가 9.8m/s^2 임을 알고 있다. 단위 통일을 위해 m대신 NM로 s(초)대신 h(시간)으로 중력가속도 값을 바꿔보면,
9.8 × 3600^2 ÷ 1852 ≒ 68578.9
중력가속도 값 g는 68578.9NM/h^2가 된다. 문제 조건에서 AOB=30˚, V=100KTS 이므로 이제 TR식에 모두 대입하면,
100^2 / 68578.9tan30˚ ≒ 0.25
즉, 선회반경은 0.25NM이 된다.
General Turning Performance 차트에서도 한번 확인 해 보자.

차트에서 선회반경은 대략 1630FT가 구해진다. 1NM이 대략 6076FT 이니, 1630FT는 대략 0.27NM이 된다. 즉, 선회반경은 0.27NM. 계산값과 비슷하게 나온것 같다. 계산값과 차트값의 차이는 대략 0.02NM, 약 37m정도 나왔다.
만약 AOB가 30˚라면, 좀 더 쉽게 선회반경(TR)을 구할 수 있는 공식도 있다. 속력만 알면 바로 선회반경을 구할 수 있다.

이 공식을 사용하여 다시 똑같은 예제를 풀어보자.
(100 ÷ 60)^2 ÷ 10 ≒ 0.28
선회반경은 0.28NM이 구해졌다. 역시 앞서 구한 TR값들과 비슷한 값이 나왔다.
이 처럼 위 공식을 사용하면, 30도 Bank 선회비행시 TR을 좀 더 간단히 구할 수 있다.
사실 AOB 30˚ 선회반경 공식에는 위 공식 외에 아래와 같은 공식이 하나 더 있는데,

또는, TR = (분당거리) - 2, 여기서 분당거리는 분속(NM/min)과 동일,
이 공식은 비행기 속도가 충분히 빠르지 않으면 정확도가 너무 떨어지기 때문에 자세히 소개하지 않았습니다. 가령 비행기 속도가 120KTAS 라면 선회반경은 0가 되며 120KTAS 이하에서는 선회반경이 마이너스 값이라는 존재할 수 없는 값이 나타납니다. 이 공식은 비행기의 속도가 대략 150KTAS 이상정도 되어야 어느정도 신뢰할 수 있으며 그 이하의 속도에서 적용하기에는 적합하지 않은 것으로 보여집니다.
참고로 150KTAS 일때 'General Turning Performance (GTP)차트' 상의 선회반경은 3,500 FT, 즉 약 0.58NM 이며, 이 계산식을 사용했을때는 선회반경이 0.5NM으로 나옵니다. <2020. 7. 14 내용 추가>
이번엔 무풍상태의 공간에서 비행기가 100KTAS로 standard rate turn(SRT) 또는 half standard rate turn(½SRT)으로 선회 중일때 TR 값은 얼마가 나오는지 구해보자.
문제를 해결하기 위해서는 먼저 SRT의 bank 요구량이 얼마인지 알아내야 한다. SRT을 위한 bank양 과 ½SRT에 필요한 bank양은 다음의 공식을 통해 구 할 수 있다.

TAS = 100KTS 이므로 대입하면 SRT bank 양은 17˚, ½SRT bank 양은 12˚가 나온다.
이제 선회반경 구하는 식을 통해 구해보면,

먼저 SRT일때,
100^2 / 68578.9tan17˚ ≒ 0.48, TR값은 대략 0.48NM 이나왔다.
다음으로 ½SRT일때,
100^2 / 68578.9tan12˚ ≒0.69, TR값은 대략 0.69NM이 나왔다.
General Turning Performance (GTP)차트를 사용해서도 구해보자.

제일먼저 'RATE OF TURN, DEGREES PER SECOND'항목에서 필요한 값을 찾는다. SRT은 초당 3˚선회율을 가지므로 '3'을 선택하였다. '3'과 TAS '100'값의 교차점에서 'BANK ANGLE FOR RATE OF TURN'항목 쪽으로 각 BANK 값과 평행하게 나아가면 SRT의 BANK 값, 대략 17˚가 됨을 확인 할 수 있다. 17˚에 해당하는 TR값은 약 3400FT, 대략 0.56NM이 나왔다.
계산값과 차트값의 차이는 0.08NM, 약 148m정도 나왔다. 뭐,.. 크게 차이 나지는 않는것 같다.
흠,.. 근데, 이렇게 GTP차트에서 일단 SRT에 관한 문제는 풀 수 있었지만, ½SRT 문제는 풀 수가 없었다. 차트에서 보다싶이 TAS '100'에서 ½SRT의 초당 1.5˚ 선회율 값을 선택하면 BANK값이 10˚값보다 작아져서 차트에서 확인이 불가능 하다. 하지만 먼저 계산식으로 구했을 때는 12˚가 나온다. 흠...
쭉쭉 잘 풀리다가,... 막혀버렸네,.... 이 현상을 어떻게 봐야할까?.....
이 글을 작성하는 나도 좀 당황스럽다.
(당연히 다 맞아 떨어질 줄 알았지,... 그래서 포스팅 작성도 오래걸렸고, 결국 떡밥을 풀지 못하고 그냥 올리게 되었다.)

이와 관련해서 잘 아시는 분이 계시면, 제게 알려주시면 감사 하겠습니다. ㅜ.ㅜ
한편, 30˚bank 공식과 마찬가지로, SRT과 ½SRT에서 선회반경을 좀더 쉽게 구할 수 있는 공식이 있다.
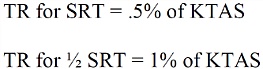
이 공식을 사용하면 SRT, ½SRT일때 TAS 값만 알면 TR값을 바로 구할 수 있다. 다시 예제를 풀어보면,
SRT일때,
TAS 0.5% = 100 × 0.5/100 = 0.5, TR값은 0.5NM
앞서 구한 계산값 0.48NM과 비슷하게 나온 것 같다. 차이는 0.02NM, 대략 37m정도.
½SRT일때,
TAS 1.0% = 100 × 1/100 = 1.0, TR값은 1.0NM이 나왔다.
앞서 구한 계산값이 0.69NM 이므로 차이는 0.31NM, 대략 574m 정도로 보인다. SRT에 비해서는 꽤 차이가 나긴 하지만 0.31NM 정도는 overshoot을 막기위한 safety margin으로 볼 수 있을것 같다. 실제 비행시에는 shallow bank에서의 adverse yaw 현상 등 선회를 방해하는 요소들을 고려하면 충분히 용인 할 수 있는 거리로 생각된다. 그리고 차라리 overshoot 보다는 undershoot 일때 그때그때 상황을 봐가며 bank량을 약간식 조절하는것이 반경을 맞추는데 더 용이 하다. 왜냐하면 bank를 더 주는 것 보다 덜 주는것이 요구되는 양력이 적고 더 천천히 돌기 때문이다.

.....그러니 일단 이 공식은 맞는것으로 치자. 이 공식이 맞아야 다음번에 쓸 글이 이어진다.
그리고 또 한편 STR 및 ½SRT의 선회반경은 완전히 다른 방식으로도 구할 수 있다. 이 방법은 선회 속도를 알고 있을 때 이론적으로 완벽한 선회반경을 구하는 방법이다.


위 공식은 STR 선회와 ½STR선회가 일정한 선회율로 구성되었다는 원리로 유도 할 수 있다. 호(arc)를 구하는 공식을 알고 있다면 위 공식에 대한 설명이 더 쉬워지지만, 완전한 이해를 도모하기 위해 원주 구하는 공식으로 위 공식을 유도 해 보겠다.
원주는 우리가 흔히 알고 있는 2πr로서 구해진다. 즉, 원의 한바퀴가 되는 각도 360˚는 2πr과 비례하는 것이다. 그리고 STR선회는 초당 3˚를 돈다. 따라서 다음과 같은식을 세울 수 있다.
2πr : 360˚ = χ : 3˚
χ는 3˚에 대한 원주이므로 1초 동안 비행기가 선회한 거리가 되겠다. 내항의 곱은 외항의 곱과 같다라는 비례식 성질을 이용해 정리하면,
(60/π) × χ = r 이 나오게 된다.
χ는 선회속도(초속) × 1초 이므로, 단위를 NM과 KT를 사용한다면 KT를 초속으로 바꿔주어야 한다.
따라서 χ는 KTAS/3600 × 1이 된다.
χ = KTAS/3600, 정리한 식에 대입하면,
r = KTAS/60π, 여기서 r이 결국 TR이므로 π를 3.14159로 놓고 정리하면 최종적으로 위 공식이 탄생하게 된다.
½STR은 3˚ 대신 1.5˚ 넣는게 되므로 그냥 2로 나누면 된다.
참고로만 알아두자. 항공사입사시험에 나온다카더라
※ 잠깐! 더 간단히 SRT 반경 공식을 유도할수 있다. (2021.07.09)
거리를 속력으로 나누면 시간이 나온다. 그러므로 거리는 원주인 2πr, 속력은 KTAS, 시간은 SRT 기준 2분을 시간으로 고친 2/60. 이제 식으로 나타내면,
2πr/KTAS = 2/60
정리하면,
r = KTAS/60π. 끝.
약식으로 KTAS/200을 대신 사용하기도 한다. 근데, 고치면 (KTAS × 0.5)/100, 결국은 TAS 0.5%다
마지막으로 '주요 선회각도에 따른 선회 시작점 부터의 수직거리'를 정리 해놓은 표를 소개한다. 선회 Lead Point 위치를 계산해야 할 때 참조하면 유용할 것이다.
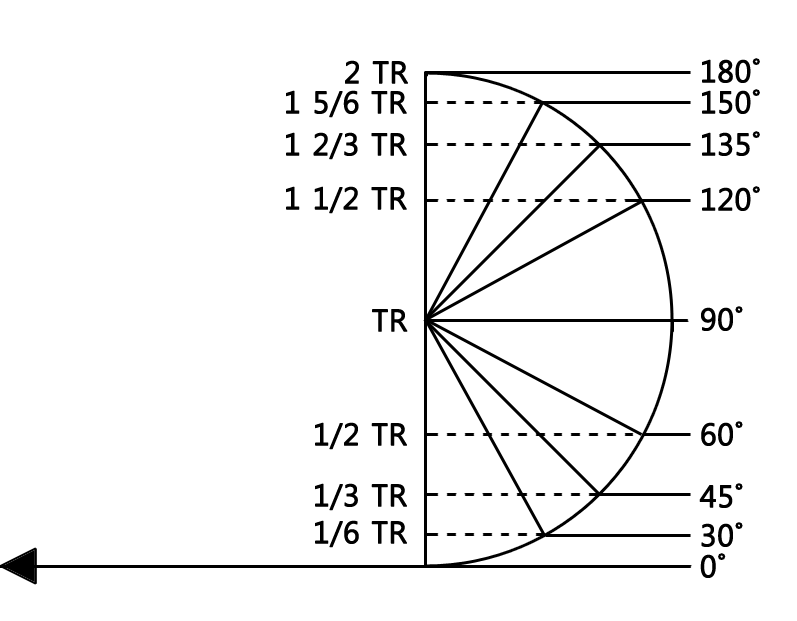
| 선회각도 |
선회 시작점 부터 수직거리 |
| 180˚ | 2 TR |
| 150˚ | 1 5/6 TR |
| 135˚ | 1 2/3 TR |
| 120˚ | 1 1/2 TR |
| 90˚ | TR |
| 60˚ | 1/2 TR |
| 45˚ | 1/3 TR |
| 30˚ | 1/6 TR |
일반적으로 선회각도 60도 미만에서는 Offset Lead Point가 작으므로 선회 시작점으로 부터의 수직거리를 신경쓰지 않아도 된다.
일단 이것으로 선회반경(또는 반지름) 계산과 관련된 글은 여기서 마치겠다.
뭐,...이렇게 마무리는 졌지만 ½SRT 선회반경에 대한 GTP차트 문제도 그렇고, 여전히 찜찜한 구석이 있다.
어째든,...
다음번에는 이 글들을 쓰게된 궁극적인 목적이기도 한 'Lead Radial(LR)' 계산에 대해 살펴보고, 그 밖에 알아두면 유용한 계산식들을 쭈-욱 정리해 보겠다. 아마 '60 대 1의 법칙(60 to 1 Rule) 과 항법계산(Aviation calculation)'의 마지막 글이 될것이다. 관련글들을 3월달 부터 쓰기 시작했건만 시간을 너무 끈것 같다. 그때 계기한정자격 막 따고서 즐거워 할때였는데,.. 지금은 어느덧 사업용 자격까지 다 따버리고 어떻게 밥벌어먹고 살지 고민중이다. 여하튼 놀고 있는동안 최대한 빨리 마무리를 지어보겠다. 자~ 그럼

오늘 하루도 GOOD DAY!
참고문헌 : AFM11-217V3
'계기비행 규칙(IFR) > 60대 1의 법칙과 항법계산' 카테고리의 다른 글
| THE AVIATION CALCULATION: DME arc 관련 계산식 (14) | 2020.07.08 |
|---|---|
| THE AVIATION CALCULATION: VVI(VSI) 계산법의 적용 (2) | 2020.07.08 |
| THE AVIATION CALCULATION: VVI(VSI)의 결정 (0) | 2020.07.08 |
| THE 60-TO-1 RULE(60 대 1의 법칙) (0) | 2020.07.08 |




