| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 국제민간항공협약
- annex14
- UAM
- 항공안전법
- Propeller
- icao
- 2007년 제3차 운송용조종사 변형
- sideslip
- dihedral effect
- dutch roll
- Turn radius
- ICAO Annex 14
- 13년도 공단 기출문제 변형
- load factor
- Lead Radial
- Best Glide Speed
- FPNM
- 2007년 제4차 자가용조종사 변형
- Today
- Total
비행사의 다이어리
THE AVIATION CALCULATION: DME arc 관련 계산식 본문
THE AVIATION CALCULATION
DME Arc (Arc-to-Radial and Radial-to-Arc) 계산식
우리나라 IAP chart 를 보면, 거의 대부분이 DME-Arc로 설계되어있다.
 |
 |
 |
 |
아마 국내에서 IFR로 비행하게 된다면 반드시 한번쯤 DME-Arc를 만나게 될 것이다. 하지만 눈에 안 보이는 이 곡선구간의 비행경로를 깔끔하게 타기란 결코 쉬운일이 아닐것이다.(하지만 G1000을 탑재하면 어떻게 될까;;)
DME-Arc로의 진입, 보통 IAF(Initial Approach Fix)에서 DME-Arc 경로가 시작된다. IAF로 깔끔하게 Direct으로 가지 않는 이상 보통은 먼저 IAF의 위치가 정의되는 Navaid(VOR 등)의 Radial을 타고(Establish) IAF까지 가게되는데, 이때 DME-Arc에 깔끔하게 진입하기 위해서 다음과 같은 공식을 사용하여 Lead Point(LP)를 잡게된다.

여기서 'TR'은 앞서 살펴본 '선회반경(또는 선회 반지름; Turn Radius; TR)의 계산'에서의 그 'TR'이 맞다.
즉, Navaid를 타고 Inbound 할때는 Arc DME + TR 이 되는 지점이 Arc turn을 시작하는 Lead Point가 되고,
Navaid를 타고 Outbound 할때는 Arc DME - TR 이 되는 지점이 Arc turn을 시작하는 Lead Point가 된다.
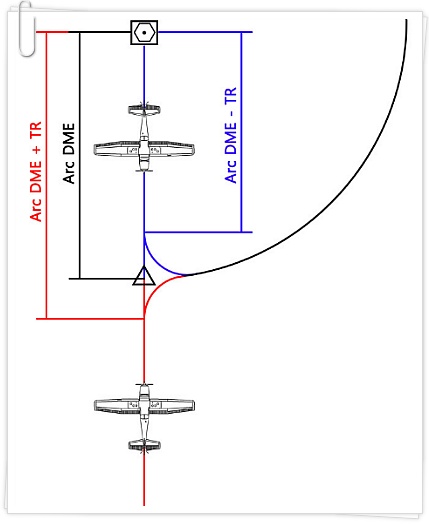
가령 무풍상태에서 100KTAS 속도로 Navaid로부터 Outbound 중이고 SRT(Standard Rate Turn)으로 10 DME Arc에 진입하고자 한다면,
TR은 TAS의 0.5%이므로 0.5NM,
Arc DME는 10,
Outbound 이므로 Arc DME - TR = 10 - 0.5 = 9.5, 따라서 LP는 9.5 DME 가 되겠다.
동일한 방법으로 Inbound시에는 LP는 10.5 DME가 나온다.
근데??, 위 그림을 다시 자세히 보자.

미묘한 α의 존재가 느껴지는가?
사실 Arc DME ± TR 지점을 LP로 잡아 Arc로 Entry turn을 하면 turn이 이루어진 만큼 처음 Entry지점에서 navaid까지 평행거리가 (α만큼)달라지기 때문에 경로가 조금 이탈 될 수 밖에 없다. 하지만 Arc 반경이 충분히 길면 오차(α)를 무시할 수 있기에 위 식과 같은 간단한 공식을 사용한다.
그러나 여기에 만족하지 않는다면,
Outbound시 계산한 DME 값보다 조금 덜 가고,
Inbound시 계산한 DME 값보다 조금 더 가서
Arc로 진입하면 좀더 깔끔하게 진입할 수 있을것이다. 물론 조금 덜 가고 더 가고 하는 이 α의 크기를 결정하는 건 조종사의 감!

자 Arc에 진입을 했으면 이제 Arc를 깔끔하게 돌기위한 뱅크를 계산해 보자.
우리는 앞서 '선회반경(또는 선회 반지름; Turn Radius; TR)의 계산' 편에서 아래와 같은 Bank(AOB)와 TR(r)의 관계식을 살펴 보았었다.

그때는 Bank에 따른 TR을 구하는것이 목적이었다면 이번에는 TR에 따른 Bank를 구하는것이 목적이 되겠다. 목적에 맞게 식을 정리하면,

,

위 와 같은 식을 유도할 수 있다.
이제 이 식을 가지고 예제를 한번 풀어보자.
> 무풍상태에서 100KTAS로 10 DME Arc turn 중, Arc turn을 유지하기 위한 Bank 량은 몇도 일까?
.
.
.
중력가속도 g는 68578.9 NM/h^2, 반경 r은 10 DME, 속도 V는 100 KTAS를 대입하고, 공학용 계산기를 두드려서 AOB값을 구해보면,
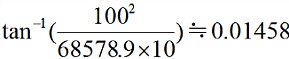
, 0.01458 radian을 구할 수 있다.
이제 radian을 degree로 바꾸기위해 계산값에 1 radian 값인 57.2958 degree을 곱하면,
0.01458 × 57.2958 ≒ 0.84, 뭐 대략 0.8~0.9도 가 나온다.
구하고 보니 AOB값이 1˚도 안된다..;;
...........흠, 이러니 10도씩 Turn & Twist 로 도나보다
이번에는 식을 좀 간소화 시켜서 예제를 다시 풀어보자. 사실 tan θ의 경우 θ값이 충분히 작으면 tanθ = θ로 둘 수 있기 때문에,

이 식을,

이렇게 바꿀 수 있다.
이제 이렇게 바꾼식에다 똑같이 중력가속도 g는 68578.9 NM/h^2, 반경 r은 10 DME, 속도 V는 100 KTAS를 대입하여 AOB값을 구해보면,

, 거의 똑같은 값이 나온다.
여기에 radian을 degree로 바꾸는 계산을 좀 더 간소화 시키고자 57.2958 대신 근사값 60을 곱하면,
0.01458 × 60 = 0.87, 역시 대략 0.8~0.9도 가 나왔다.
이것을 공식화 시키면 다음과 같이 나타낼 수 있다.

근데 여기서 조금만 더 식을 비틀면,

2V^2 / g를 뽑아낼 수 있다. 이것을 Bank(AOB)와 TR(r)의 관계식으로 해석 해보면,

tan(AOB) = 1/2라는 결론을 이끌어 낼 수가 있고 1/2값이 되는 탄젠트 각(AOB)을 찾아보면,

약 27도가 나오는데 30도랑 0.0679정도 밖에 차이가 안난다. 때문에 위 식 2V^2 / g를 AOB 30도일때 TR로 처리해 간소화 시키면,

,
최종적으로 아까보다 더 간단한 공식을 이끌어 낼 수 있다.

이 식으로 한번 더 위 예제를 풀어서 구한 Bank값이 비슷하게 나오는지 확인해 보자.
( 30 ÷ 10 ) × TR
여기서 TR은 30˚Bank turning circle의 반경이므로 앞서 '선회반경(또는 선회 반지름; Turn Radius; TR)의 계산' 편에서 살펴본 공식으로 TR을 구해보면,
TR = ( TAS ÷ 60 )^2 ÷ 10 = ( 100 ÷ 60 )^2 ÷ 10 ≒ 0.28
그러므로,
( 30 ÷ 10 ) × TR = (30 ÷ 10 ) × 0.28 = 0.84
앞서 풀어보았던 방식과 거의 동일하게 Bank값이 0.84˚가 나오는 것이 확인되었다. 이렇게 검증까지 끝났다.
.
.
.
.

근데 0.8~0.9도 bank를 조종하는것이 과연 의미가 있을까? 자세계 오차를 5도까지 허용하는마당에.., 이것을 미세하게 조종해서 맞추는것은 거의 불가능에 가깝다. 더군다나 Adverse Yaw 현상까지 생각해 보면 답이없다. 따라서 그럴때는, 우리가 통상적으로 쓰는, Radial 과 DME를 확인하면서 10˚ 식 끊어서 도는 방법을 쓸 수 밖에 없는 것 같다.
내가 이 글을 쓰면서 계속 참고하고 있는 'AFM11-217V3'(71 페이지 참조) 에서도 이 Arc 돌때 필요한 Bank 구하는 공식은 '빡쎈(tight)' Arc를 돌때 필요할것이라고 적혀있다. 그럼 그 빡센 Arc가 뭐냐, 속도가 빠른 비행기가 작은 반경의 Arc를 돌때, 바로 그 Arc를 말한다. 왜냐하면 비행기 속도가 빠르거나 DME 반경이 작으면, 그만큼 Arc를 도는 각속도가 빨라지고 이에따라 Radial 변화가 너무 빨라 10˚씩 끊는 Turn & Twist 를 수행하기에 애로사항이 꽃피기 때문이다.
> 자 이번엔 좀 빡쎌것 같은 Arc, 6 DME Arc를 무풍상태에서 200KTAS로 돌때 필요한 Bank량을 구해보자.
TR = ( TAS ÷ 60 )^2 ÷ 10 = ( 200 ÷ 60 )^2 ÷ 10 ≒ 1.1, 1.1NM,
Required Arc Bank Δ = ( 30 ÷ DME ) × TR = (30 ÷ 6 ) × 1.1 = 5.5, 5.5˚가 나왔다. 대략 Bank를 5~6˚ 사이로 유지해서 Arc를 돌면 되겠다.

이렇게 Arc를 깔끔하게 다 돌았으면 이제 산듯하게 Radial 코스(Course)를 타고 Arc를 빠져나가기 위해 대망의 'Lead Radial'을 계산해 보자!!

저 붉은색 박스안의 LR(Lead Radial)이 보이는가? 과연 무슨 근거로 Approach Chart에 195 Radial 이라고 적어 놓았을까? 이 최초의 떡밥을 풀기 위해선 마찬가지로 제일 처음 저~ 앞에서 살펴본 '60 대 1의 법칙(60 to 1 Rule)'을 복기할 필요가 있다.
다시 60 대 1의 법칙(60 to 1 Rule)...

1˚, 즉 1 Radial 이 60NM 밖에서 1NM이 되는 원리. 만약 현재 비행속도에서 TR이 1NM인 비행기가 60 DME Arc를 타고 있다면 LR은 1NM이 되는 1 Radial 전 이되는것이다 (아래 파란색 경로).

동일한 조건에서 이번엔 Arc 반경만 30 DME로 줄이면 TR 1NM에 해당하는 각이 커짐으로 2 Radial 전이 LR이 된다 (아래 붉은색 경로).

따라서 이와같은 관계는 'Radials per NM' 이라는 관계식으로 나타낼 수 있다.

여기서 'Radials per NM'은 TR = 1NM 인 특수한 경우를 나타낸 것이라고 볼 수 있다. 만약 TR = 2NM 로 커지면 Arc상에서도 2NM 전에 Lead Point 를 잡아야 하기 때문에 LR이 2배로 커져버릴 수 밖에 없는데, 이처럼 TR이 커지면 LR도 그에 비례하여 커지기 때문에 (아래 자주색 경로),

'Radials per NM'에 'TR'을 곱하여 다음과 같은 보편적인 LR공식이 나오는 것이다.

드디어 나왔다! LR공식!

내가 60 대 1의 법칙 과 항법계산들을 찾아보게 만든 그 공식, 그리고 이 글을 여기까지 쓰게 만든 원동력!
맨 처음 글에서 에서 "60을 DME로 나누고 진대기속도(TAS)의 1%를 곱하면 LR이 나온다"라고 교관님이 내게 알려주셨던 공식이 바로 이 공식이였던 것이다. 즉, '60을 DME로 나눈다' 라고 한 건 Radial per NM을 구하는 것이였고, '진대기속도(TAS)의 1%를 곱한다'고 한 건 바로 앞글에서 살펴본 ½SRT에서의 TR을 곱하는 것이였다.
그래서 이 공식이 무안 VOR 15 DME Arc 를 100KTAS 돌 때 LR을 4 Radial로 잡을 수 있는 근거가 되는 것이다.

그럼 이 LR 195, 이것은? (아직 안끝났음 -_-;;)
Arc를 빠져나가는 코스 Radial 이 187˚ 이므로 LR은, 195 - 187 = 8, 8 Radial 이전이 된다.
일단 AFM11-217V3 에는,

보통 차트에서는 240KTAS, TR 1~2NM 기준으로 LR를 잡아 표기한다고 한다. 물론 TERPs 기준이라 우리나라가 채택하고 있는 PANS-OPS 기준과 좀 차이가 있을지 모르지만, 어째든 이것을 근거로 LR 195 가 어떻게 나왔는지 확인해 보자.
먼저 Radials per NM.
15 DME Arc 이므로 60 ÷ 15 = 4
다음으로 TR.
LR 이 8 Radial 이전 이므로 4×TR이 8이 되기 위해선 자동적으로 2NM가 되어야 한다.
자, 그럼 이 TR = 2NM.
속도를 240KTA로 가정했을때 선회 AOB 구하는 공식에 넣어보면 (g는 68578.9 NM/h^2),

tan^-1( 240^2 / (68578.9 × 2) ) ≒ 0.4 rad, degree로 고치면, 대략 23˚ Bank가 나온다.
240KTAS로 23도 Bank 턴이라.......SRT Bank가 아닐까 예상했는데 아닌것같다. 아니면 애초에 240KTAS 기준이 아닌지도 모르겠다.
그러면 다른 IAP 차트를 한번 볼까?
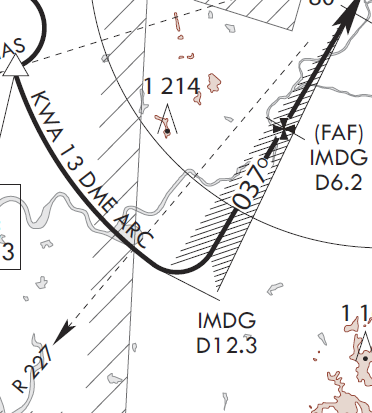
광주공항.
R 227 - R 217 = LR 10
60 ÷ 13 DME ≒ 4.6, 10 ÷ 4.6 ≒ TR 2NM
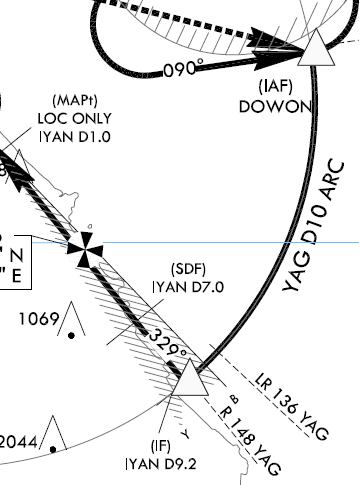
양양공항.
R 148 - R 136 = LR 12
60 ÷ 10 DME ≒ 6, 12 ÷ 6 = TR 2NM

울산공항
R 184 - R 172 = LR 12
60 ÷ 10 DME ≒ 6, 12 ÷ 6 = TR 2NM
흠, 결론은 TR = 2 NM 기준으로 차트 LR을 표기하는것 같다는 것이다. 따라서 저 무안차트에 나온 LR 195는 선회반경이 2 NM 정도 나와주는 비행기를 위한 LR인셈이다.
그리고 결정적으로, TR = 2 NM 기준으로 차트에 LR이 그려진다는 내용이 PANS-OPS(Doc 8168) Vol. II에 나와있다.

즉, Arc설계시 Arc에서 다른 경로로 이어질때 그 각이 120˚를 넘어선 안되며, 만약 70˚를 넘는다면 2NM의 선도점을 가지는 Lead Radial이 제공되어야 한다는 것이다. 따라서 위 에 나열된 Arc들 모두 90˚ 경로로 이어지므로 2NM의 선도점을 가저야 하므로 TR = 2NM 가 구해졌던 것이다.
.
.
.
LR계산 이라는 교관님의 던진 작은 떡밥에서 시작된 60 대 1의 법칙(60 to 1 Rule), 그리고 항법계산(Aviation calculation)에 관한 탐구는 이렇게 끝이 났다.
이 5편의 글을 쓴 목적은 비행공부 했던 내용을 되새겨 보고 정리해보기 위한 목적과 비슷한 문제로 고민하는 사람들과 정보를 공유하고 싶었기 때문이다. 근데, 글 올라오는 속도가 너무 느려서 얼마나 많은 분들에게 참고가 되었는지 모르겠다 (보다가도 지쳐서 포기하셨을 듯..).

글 쓰기는 참 어렵다...
여하튼 끝까지 읽어주셔서 감사 ㄳ.
참고문헌 : AFM11-217V3
'계기비행 규칙(IFR) > 60대 1의 법칙과 항법계산' 카테고리의 다른 글
| THE AVIATION CALCULATION: 선회반경(선회 반지름)의 계산 (4) | 2020.07.08 |
|---|---|
| THE AVIATION CALCULATION: VVI(VSI) 계산법의 적용 (2) | 2020.07.08 |
| THE AVIATION CALCULATION: VVI(VSI)의 결정 (0) | 2020.07.08 |
| THE 60-TO-1 RULE(60 대 1의 법칙) (0) | 2020.07.08 |




