| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- FPNM
- sideslip
- 2007년 제4차 자가용조종사 변형
- annex14
- load factor
- UAM
- Best Glide Speed
- dutch roll
- 항공안전법
- Propeller
- Lead Radial
- icao
- Turn radius
- 국제민간항공협약
- 13년도 공단 기출문제 변형
- 2007년 제3차 운송용조종사 변형
- ICAO Annex 14
- dihedral effect
- Today
- Total
비행사의 다이어리
상반각(dihedral angle)에 대한 오류, 그리고 그것을 해결하는 Dihedral effect 본문
상반각(dihedral angle).


비행기를 정면에서 보았을때 수평면 위로 좌우 날개가 V자 형태로 하늘을 향해 올라간 각. 주로 날개가 동체 아래에 위치한 저익기에서 보이는 이 멋스러운 날개각은 비행기의 미관을 더해주기도 하지만 근본적으로 '가로안정성'을 위해 설계된다.
가로 안정성(Lateral stability)?

비행기 기축선(종축)을 중심으로 움직이는 비행기 운동에 대한 안정성, 즉 롤링(Rolling) 운동에 대한 안정성(Stability)이라는 뜻한다. 상반각은 이러한 롤링 운동에 대해서 안정적으로 원래의 수평상태로 되돌아가려는 소위 '복원력(또는 복원모멘트)'을 제공한다.
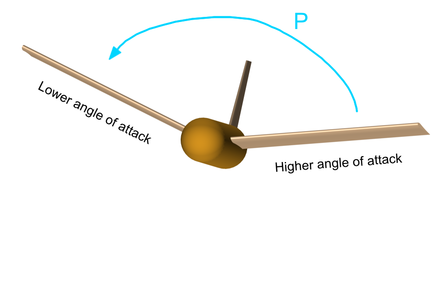
그럼 어떻게 '복원력'이 생기는가??

상반각은 위 그림처럼 비행기를 떠받치는 양력을 오히려 저하시킨다. 상반각으로 인해 날개에서 만들어지는 양력의 방향이 기울어지게 되므로 수평성분(Lx)과 수직성분(Ly)이 나타나게 되고 여기서 비행기를 떠받치는 양력의 수직성분을 제외한 수평성분 만큼의 양력 손실이 생기게 된다.
그럼, 이 수평성분(Lx)가 복원력을 만드는 것일까?

비행기가 롤링(Rolling)으로 날개가 기울어 졌을 때 확실히 중력에 대항하는 양력의 수직성분(Ly)은 감소한다. 그래서 비행기가 한쪽으로 기울게 되었을 때 수평비행을 유지하려면 조종간을 더 당겨서 받음각(AOA)을 높여 양력을 증가시켜야 한다. 그래서 상반각 또한 비슷한 원리로 생각하여 위 그림과 같이 상반각을 가진 비행기가 기울어졌을 때 올라간 날개의 양력의 수직성분 성분이 감소하여 수평상태로 다시 되돌아 올 것이라고 착각하기 쉽다.
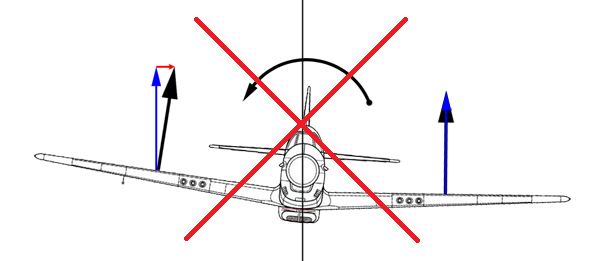
하지만 이것은 모멘트(Moment)를 간과한 잘못된 해석이다.
가령 사고 실험을 위해 상반각을 가진 비행기가 기울어져도 양쪽 날개의 양력의 수직성분은 동일하다고 가정해 보자.

만약에 양력의 수직 성분의 차이로 복원력이 생긴다는 논리가 맞으려면 저 상태에서는 복원력이 없기 때문에 그 상태를 유지해야 한다. 하지만 회전축에 작용하는 모멘트를 가지고 해석하면 비행기는 더 기울어진다는 결론이 나온다.
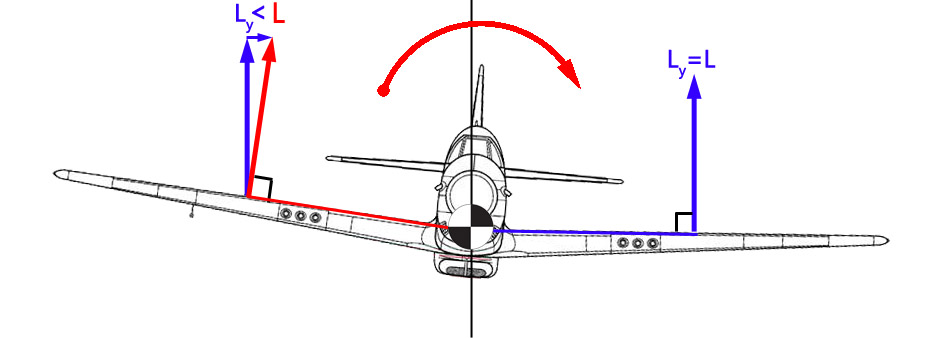
왜냐하면, 모멘트에서 힘은 회전축에 90도로 작용하는 힘이기 때문이다.
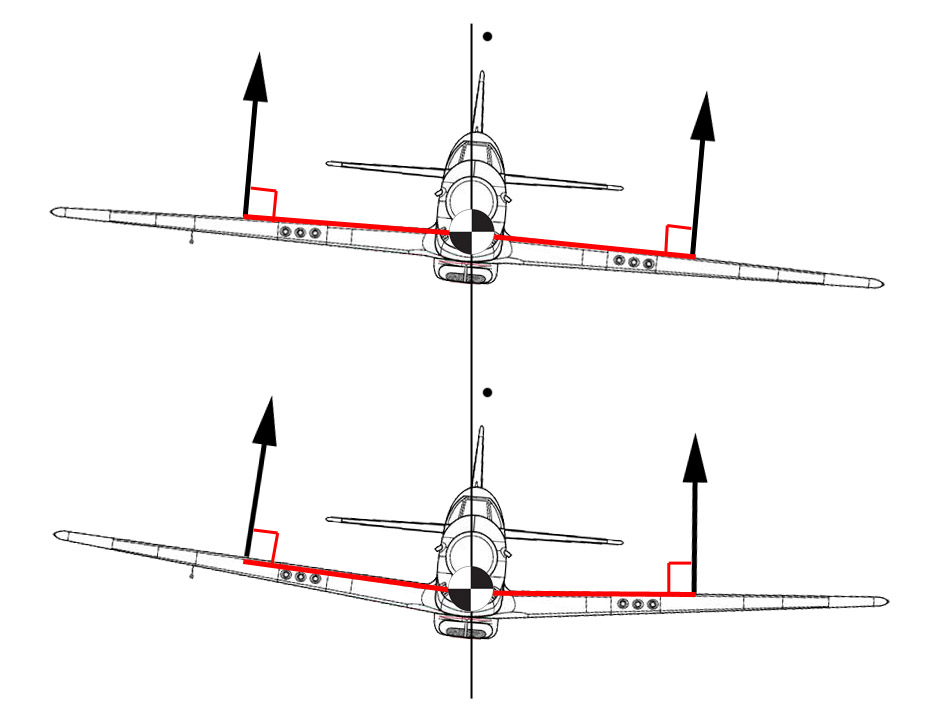
따라서 상반각이 더 커지든 작아지든 양쪽 날개의 모멘트는 항상 같을 수 밖에 없다. 즉, 수평상태로 다시 못 돌아 온다는 이야기다. 이런 식으로는 가로안정성의 복원력을 설명할 수 없다.
마찬가지로 인터넷 상에 떠돌아 다니는 아래와 같은 상반각의 원리를 설명하는 그림들,


이러한 날개의 투영면적을 비교하는 방법으로도, 역시 상반각에 의한 가로안정성을 설명할 수 없다.
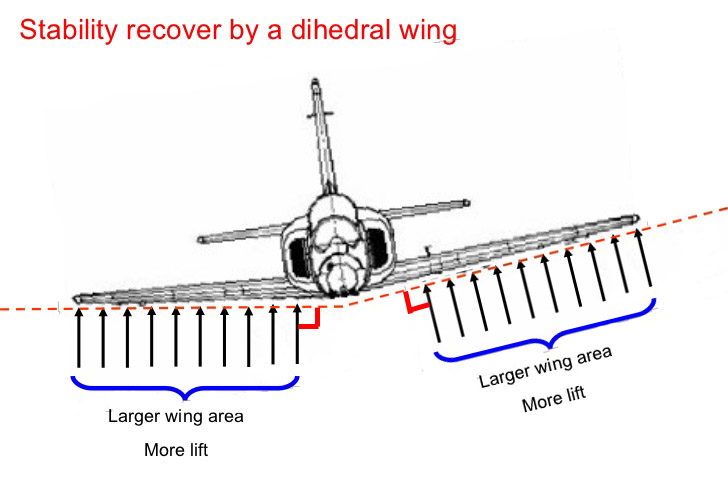
왜냐하면 3차원의 공간에서 비행기가 기울든 세워지든 뒤집어지든 공기와 맞 닿는 날개 면적은 양쪽 모두가 같고 항상 동일한 양력이 발생하기 때문이다. 그리고 양력 또한 양쪽 날개 모두 회전축을 중심으로 서로 마주보며 90도 방향으로 작용하기 때문에 복원력이 나타날 수 없다. 따라서 투영면적을 비교하는 것 자체가 의미가 없다.
.
.
그래서 그런가?
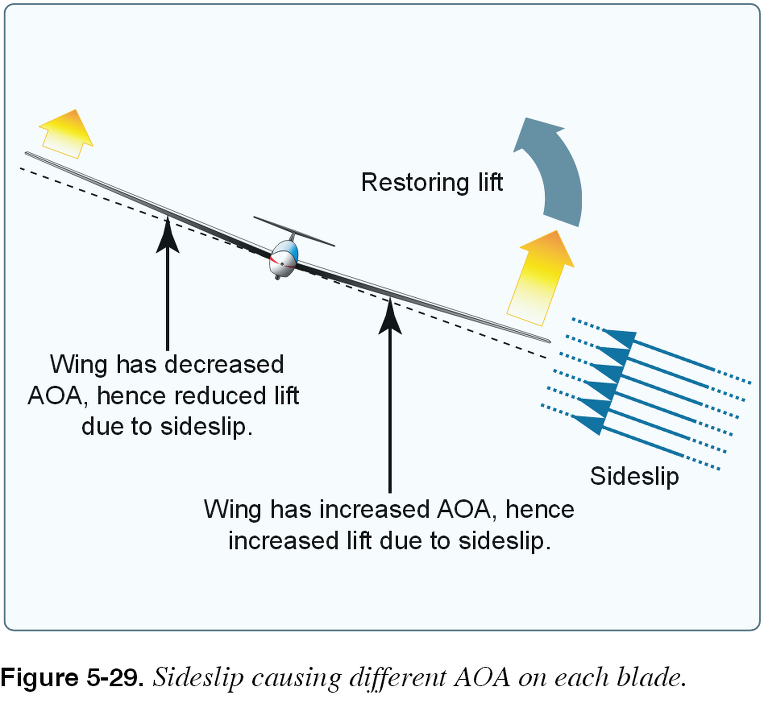
모든 공식적인 교재들이 '사이드슬립'과 그로인해 발생하는 양 날개의 'AOA 차이'로 상반각에 의한 가로안정성의 복원력(복원모멘트)을 설명한다.
위 그림은 FAA에서 발간한 'Pilot's Handbook of Aeronautical Knowledge'라는 책자(18페이지)에서 상반날개(dihedral)와 가로안정성에 대해 설명할때 등장하는 그림이다. 그림을 살펴보면 사이드 슬립(Side slip)과 이로 인해 생기는 양 날개의 AOA 차이를 통해 상반날개의 효과에 대해 설명하고 있음을 알 수 있다.
그런데 문제는 내 머리로는 상반날개에 사이드 슬립을 걸 때 도대체 왜 좌우 날개의 AOA가 서로 차이가 나게 되는지 도무지 알수가 없다는 점이었다.
저 그림(Figure 5-29.)만 봐도 조금만 삐딱하게 보면,

측풍에 홱까닥 뒤집히는 형상으로 밖에 안보이는데, 여기서 어떻게 가로 안정성이 나올 수 있을까??
아래와 같이 인터넷에서 dihedral을 설명하는 수만은 그림을 봐도 AOA변화로는 도저히 이해가 불가능 했다.
 |
 |
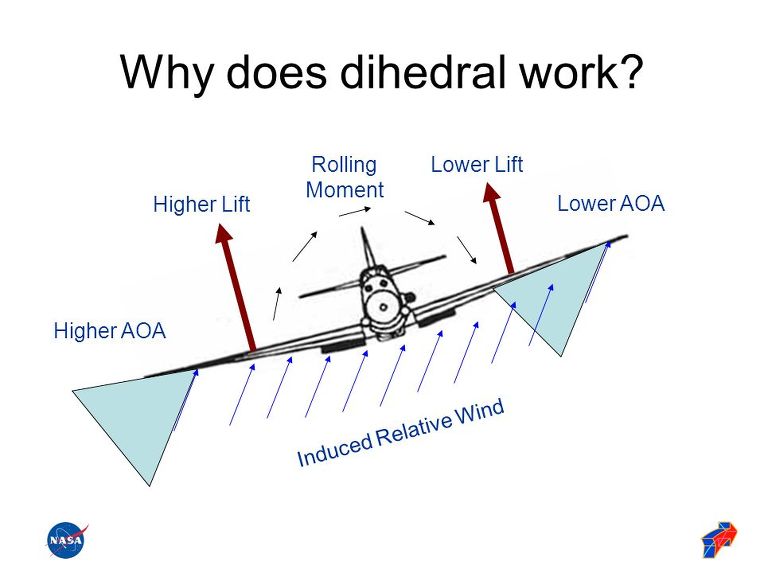
몇몇 그림은 AOA 차이는 이해가 가도 상대풍의 방향은 납득할 수 없었다. 대부분이 상대풍의 방향이 아래에서 위로 비스듬히 올라오는 형태로 그리고 있는데 비스듬히 정면으로 받는 바람이라고 상상을 하 AOA차이가 표현이 되지 않는다. 오히려 Sweepback을 묘사하는 것 같아 보인다.
내 나름대로도 dihedral 설명을 여러번 곱씹어 보며 어떻게든 상대풍과 상대풍, 그리고 AOA 간의 관계를 그림으로 표현해 보려고 했지만 모두 실패하였다. 그리고 여러번의 시도끝에 이 모든 문제들이 결국 3차원 문제를 무리하게 2차원으로 표현하려는데서 비롯된 것임을 깨닫게 되었다.

Dihedral effect, 그리고 3차원적 문제
'Pilot's Handbook of Aeronautical Knowledge'(이하, PHAK)에서는 상반각을 'Dihedral effect'에 기반하여 설명하고있다. 이 것은 해당 내용의 마지막 구절인 "dihedral contributes to a stable roll due to sideslip"라는 문구에서 잘 드러난다.

SIDE SLIP, 그렇다 'Dihedral effect'에서 가장 중요한 요소는 바로 SIDE SLIP이다. '위키백과'에서도 사이드 슬립 각(Side slip angle)이 '0' 이 아닐때 생기게 되는 롤링 모멘트로 설명하고 있다.
즉, 좀더 쉽게 풀어서 말하면 Dihedral effect 란 사이드 슬립 도중 기울어져 있는 날개에 롤링 모멘트가 발생하는 현상인것이다. 그리고 그 롤링 모멘트가 좋은쪽으로 작용하면 가로 안정성을 높이는 복원력이 되는것이었다..
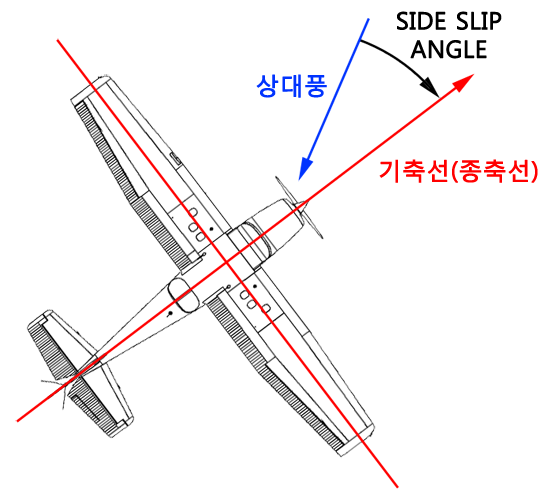
그렇다면 사이드 슬립은 언제 일어날까?


대표적인 경우로 측풍착륙시 인위적인 사이드 슬립을 만드는 'WING LOW METHOD'를 들 수 있다. 비행기가 착륙시 측풍이 불게되면 위 그림과 같이 바람을 비스듬하게 받게되는데, 이때 바람에 밀리지 않게 풍상측 날개를 내리고(Wing low) 기수가 틀어지지 않도록 반대방향으로 러더를 차면, 비행기는 딱! 위 그림과 같은 모양세가 된다.
근데 여기서 잠깐! 측풍이 불 때 그냥 기축선만 똑바로 유지한채 수평비행을 해도 저런 모양이 나오지 안을까 헷갈릴 수도 있다. 왜냐면, 측풍이 부니깐 측풍이랑 기축선 사이의 각을 'SIDE SLIP ANGLE'로 볼 수 있지 않는것 아닌감, 하고 생각해 버릴 수 있기때문.

그러나 'SIDE SLIP ANGLE'을 이루는 요소가 단순한 측풍이 아니라 '상대풍'이기 때문에 이것은 옳지 않다. 단순히 측풍에서 수평비행하게 되면 위 그림처럼 상대풍은 정풍에서 받는것이 되고 SIDE SLIP ANGLE 은 0 도가 되기 때문에 사이드 슬립과 전혀 무관하다. 너무 당연한 이야기다. 바람이 어느쪽에서 불 건 삼타일치(coordinated) 되어있는 수평비행 중에는 SLIP IND'의 볼이 튀지 않는다.
어째든 이와 같이 사이드 슬립 중인 비행기는, WING LOW METHOD를 직접 체험 해 보면 알겠지만, 풍상측으로 내린 날개가 자꾸 되돌아 올라 오려고 한다. 나는 이것이 바로 'Dihedral effect'라고 생각한다.
문제는 앞에서도 이야기 했지만 이 롤 현상을 2차원으로 표현하는것이 쉽지 않다는 점이다.
그래서,
.
.
처음으로 3D 캐드를 이용해 3차원으로 이 롤 현상을 설명해 보기로 했다.

먼저 위 그림처럼 평평한 날개를 대충 3D로 그려놓은 다음,
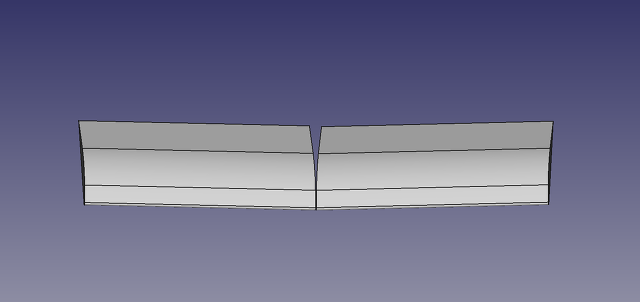
여기에 상반각을 주고,...
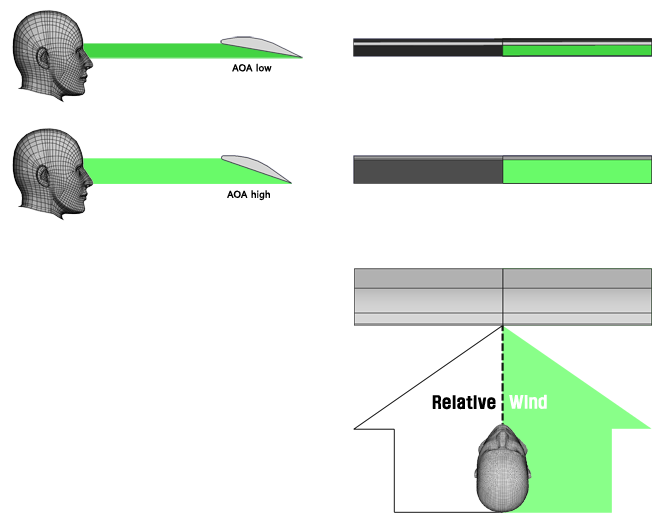
위 그림 처럼 상대풍을 정면에서 받고 있다고 가정하고 날개를 상대풍의 시점인 정면에서 쳐다보았을때 AOA가 클수록 눈에 보이는 날개 밑면의 면적도 같이 커지는 원리를 이용하여 상반각을 가진 비행기가 사이드 슬립상태에 있을때 날개의 AOA가 어떻게 되는지 확인해 보았다.
사이드 슬립 상태에서는 상대풍이 비행기 기축선을 중심으로 SIDE SLIP ANGLE 만큼 비스듬히 불기때문에 상대풍 시점도 비행기를 비스듬히 바라보는 위치가 된다. 따라서 다음 그림과 같이 볼 수 있는 모습이된다.
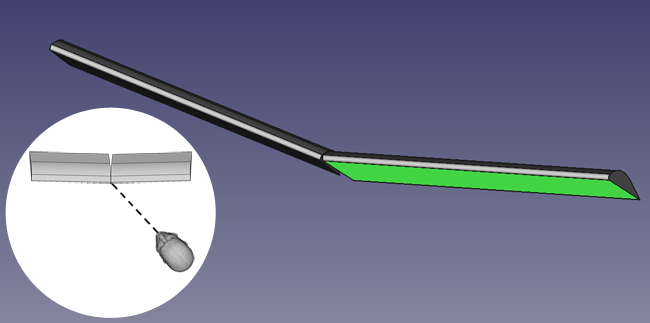
보다시피 아래로 쳐진 날개의 밑면(녹색면적)이 올라간 날개보다 밑면보다 더 넓게 보인다.
반면 상반각을 주지 않았을 때는,

쳐진 날개나 올라간 날개나 보이는 면적이 동일하다.
즉 상반각을 주지 않으면 사이드 슬립 상태에서 기울어져 있는 양쪽 날개의 AOA가 동일하기 때문에 Dihedral effect는 나타나지 않는다. 그러나 상반각을 주게되면 사이드 슬립 상태에서 기울어진 양쪽 날개 중 아래로 쳐져 있는 날개의 AOA가 더 크기 때문에 그만큼 양력을 더 많이 가져감으로써 롤링 모멘트가 생기게 되는데, 이것이 바로 진정한 상반각으로 만들어진 'Dihedral effect' 인 것이다!
사이드 슬립은 WING LOW METHOD 같은 인위적인 경우가 아니더라도 바람이 급변하는 환경 등으로 언제든지 자연스럽게 만들어 질 수 있다. 그리고 그와같은 환경속에서 상반각을 가진 비행기는 바람에 의해 강제적으로 날개가 기울어져 슬립이 일어나도 동시에 Dihedral effect 가 발생하여 스스로 원 상태로 돌아 갈 수 있는 복원력을 얻게 되는 것이다.
그 과정은 아마도 쓰러진 오뚜기가 다시 일어서는 것과 같을 것이다.

To be continued...
'비행 관련 기타' 카테고리의 다른 글
| 2021서울 ADEX, 무인기 시대의 서막을 알리다.(스압) (0) | 2021.10.24 |
|---|---|
| STANDARD RATE TURN 뱅크 계산식 분석 (7) | 2021.07.28 |
| Vg 다이어그램을 그려보자! (4) | 2021.06.16 |
| 최대활공거리가 항상 일정한 이유 (15) | 2021.05.24 |
| 양항비, 양력(LIFT)과 항력(DRAG)의 비(RATIO), 언제 최대가 될까? (수정) (8) | 2020.08.14 |