STANDARD RATE TURN 뱅크 계산식 분석

 

먼저 글쓰기 소재를 제공해 주신 김영헌님께 감사드립니다!

 

그럼, STANDARD RATE TURN의 뱅크(BANK) 계산식 분석, 바로 시작하겠습니다!

 

 

 

---

 

1단계, 진짜 STANDARD RATE TURN의 뱅크 계산식

 

STANDARD RATE TURN(이하 SRT)의 정확한 뱅크량을 구하기 위해서는 항법계산(선회반경 계산 편) 글에서 다루웠던 선회반경을 구하는 공식을 사용해야 합니다. 

 

AOB: Angle Of Bank

mgtan(AOB)=구심력

 

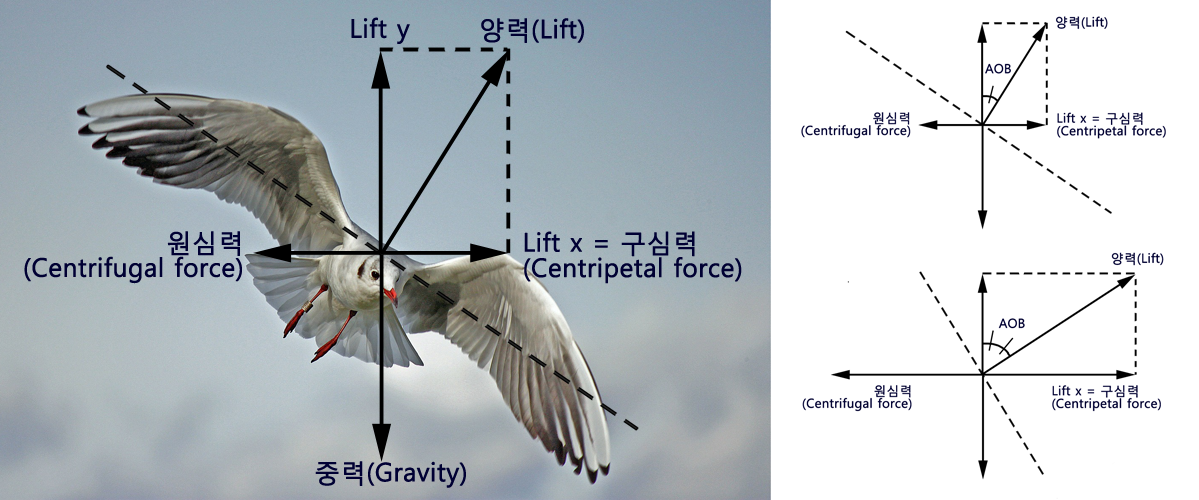
선회반경을 구하는 공식에 SRT의 선회반경을 대입하여 정리하면, 이론적으로 가장 정확한 SRT의 뱅크를 구할 수 있기 때문입니다. 따라서 먼저 SRT의 선회반경을 구해야 하는데요, 이론적으로 완벽한 SRT의 뱅크를 구해야 하기 때문에, TAS의 0.5% 같이 대충 계산하는 방법은 쓰지 않겠습니다. 대신 이론적으로 완벽한, 아래와 같이 구해진 SRT의 선회반경을 사용할 것입니다.

 

거리를 속력으로 나누면 시간이 나온다. 그러므로 '거리'는 원주인 2πr, '속력'은 TAS, '시간'은 SRT 기준 2분을 시간으로 고친 2/60. 이제 이 조건들을 관계식으로 나타내면,

2πr/TAS = 2/60

정리하면,
r = TAS/60π.

이론상 가장 완벽한 SRT 선회반경

 

이제 이 식들을 서로 연결하여 정리하고,

 

 

여기서 중력가속도 g ≒ 68578.9NM/h^2

 

정리된 식을 탄젠트 함수의 역함수(아크탄젠트)로 만들어주면,

 

 

 

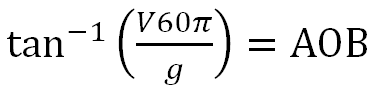
이론적으로 가장 완벽한 SRT 뱅크 구하는 식이 완성 됩니다.

 

 

---

2단계, 그래프로 경향 파악

 

이상적인 SRT 뱅크 구하는 정밀 계산식을 완성했으면, 속도별로 BANK 값을 구하여 그래프를 그리고 그 경향과 추세를 파악해볼 것입니다. 그리고 약식인 (TAS/10) + 7의 그래프와도 비교를 해봄으로써 약식이 어떻게 만들어졌는지 조심스럽게 한번 파악해 보겠습니다.

 

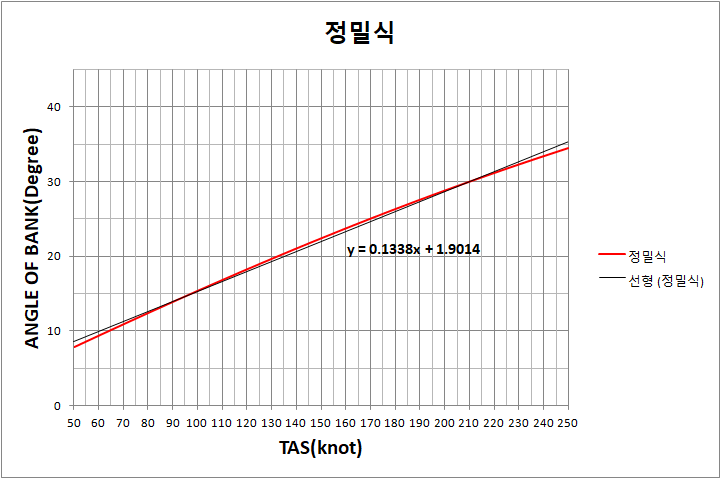
먼저 1단계에서 구한 정밀식의 그래프 입니다. 속도 범위는 0 부터 600 knots까지로 설정하였습니다.

 

 

 

그래프가 직선은 아니지만 직선의 경향성을 가진 미묘한 곡선인 것을 볼 수 있습니다. 혹시 1차 함수(선형)로 근사시키면 약식이 바로 나오는지 확인하기 위해 직선(1차 함수, 선형)이 되는 추세선을 한번 그려보겠습니다.

 

 

 

추세선을 나타내는 식 "0.0969TAS + 6.8797" 이 약식 0.1TAS + 7과 매우 닮아보입니다. 그렇다면, 이번엔 약식 그래프를 추가하여 정밀식의 추세선과 약식의 경향성이 얼마나 닮았는지 눈으로 직접 확인해 봅시다.

 

 

파란색 선이 약식을 나타내는 그래프이다.

 

굉장히 유사합니다. 왠지 속도 범위만 잘 조절하면 정밀식의 추세선을 약식을 나타내는 함수 "y = 0.1x +7"에 맞출 수 있을 것 같기도 한데, 확신은 없습니다. 중요한 것은 SRT 뱅크 구하는 정밀식의 추세선이 일정 속도 구간에서 SRT 뱅크 구하는 약식과 비슷하게 나온다는 점입니다.

 

어쩌면 계산상의 편의를 위해 특정 구간(0~600 knots)의 추세선 함수를 간소화 시킨것이 우리가 지금 SRT 뱅크 계산에 쓰는 약식일지도 모른다는 생각을 해 봅니다(뇌피셜 유의).

 

 

728x90

---

 

결론

 

정밀식을 1차 함수로 근사시킨 추세선은 속도의 범위에 따라서 달라집니다. 왜냐하면 정밀식이 직선이 아닌 곡선이기 때문에 각 구간별 직선의 기울기가 모두 다르고, 절편 또한 다르기 때문입니다.

 

 

속도 50~250 knots 구간에서의 정밀식의 추세선, 추세선 함수의 절편 1.9014가 약식의 절편 7과 차이가 많이 난다.

 

이 말은 우리가 쓰는 SRT 뱅크 약식 또한 비행기를 운항하는 속도 구간이 어디냐에 따라서 정확도가 달라질 수 있다는 의미입니다. 아래 그래프는 약식 "0.1TAS + 7"에서 절편 7을 각각 6, 5로 바꾸어 그려본 그래프 입니다.

 

 

 

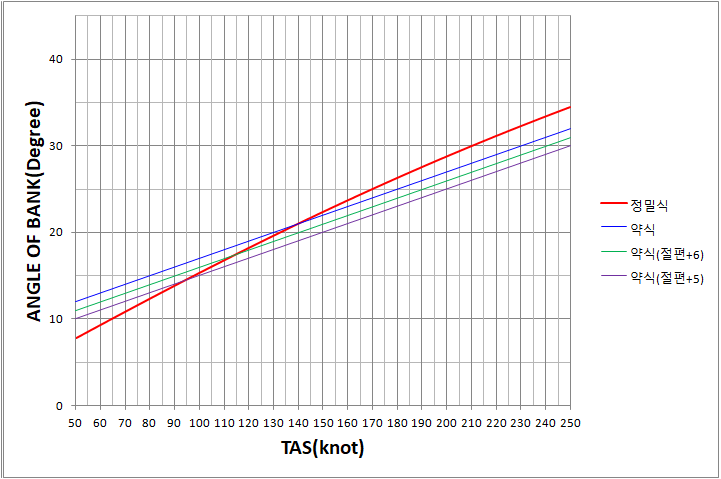
보다시피 TAS 50~110 knots 구간에서는 "0.1TAS + 5" 식(보라색)이 오히려 "0.1TAS + 7" 식(파란색)보다 SRT 뱅크를 더 정확하게 구할 수 있습니다. 그리고 TAS 100~125 knots 구간에서는 "0.1TAS + 6" 식(초록색)을 쓰는 것이 더 적절할 것입니다.

 

그럼에도 불구하고 "0.1TAS + 7"식을 쓰는 것은 85 knots 이상 240 knots 이하 넓은 속도 범위에서 약 2도 정도의 오차 범위 내에 있기 때문에, 모든 항공기에 보편적으로 적용할 수 있어서 그냥 쓰는 것 같습니다(뇌피셜 유의). 사실상 계기비행을 하는 비행기 중 85 knots 이하로 운항하는 비행기는 거의 없고, 또한 210 knots만 초과하게 돼도 SRT 뱅크가 30도를 넘어가기 때문에 240knot 이상 속도에서 SRT을 쓸 일은 아마도 없을 것입니다.

 

ICAO Holding bank 요건, 25도 뱅크와 SRT 뱅크 중 작은 것을 사용한다. (출처: DOC8168 VOL.1)

 

FAA Holding bank 요건, SRT 뱅크와 30도(25도) 뱅크 중 가장 작은 것을 사용한다.  (출처: AIM)

 

 

 

지금까지 STANDARD RATE TURN의 뱅크(BANK) 계산식을 분석해 보았습니다. 혹시, 글에서 논리 전개 과정에 오류가 있거나 설명에 이해가지 않는 부분이 있다면 댓글 등을 통해서 편하게 알려주시기 바랍니다. 이 글에서 설명하는데 사용했던 그래프 차트 및 뱅크 계산식의 데이터는 아래 첨부된 엑셀파일에 담겨있습니다.

 

Standard Rate Turn Bank Graph.xlsx

0.16MB

 

질문자님의 궁금증 해소에 적게 나마 도움이 되었으면 합니다.

 

감사합니다.