| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Turn radius
- sideslip
- UAM
- FPNM
- 2007년 제3차 운송용조종사 변형
- 2007년 제4차 자가용조종사 변형
- annex14
- 13년도 공단 기출문제 변형
- dihedral effect
- Lead Radial
- Best Glide Speed
- ICAO Annex 14
- icao
- Propeller
- 국제민간항공협약
- dutch roll
- 항공안전법
- load factor
- Today
- Total
비행사의 다이어리
최대활공거리가 항상 일정한 이유 본문
왜? 비행기의 무게가 증가해도 최대활공거리는 일정할까?
Variations in weight do not affect the glide angle provided the pilot uses the proper airspeed. Since it is the L/D ratio that determines the distance the airplane can glide, weight does not affect the distance flown.
(인용 출처: Airplane Flying Handbook, FAA-H-8083-3B, Chapter 3: Basic Flight Maneuvers, Glides(p3-20))

최대활공속도(BEST GLIDE SPEED)는 최대활공속도는 양력과 항력의 비(이하 양항비)가 최대가 되는 지점의 속도이며,
이러한 양항비가 최대가 되는 지점은 전체항력이 가장 작은, 유도항력과 유해항력이 정확하게 똑같아지는 지점이다.

그리고 비행기의 무게가 증가하면 유도항력이 증가하기 때문에 유도항력과 유해항력이 똑같아지는 지점의 속도는 커지게 된다.
다들 여기까지는 이해하는 데에는 큰 문제가 없을 것이다.
하지만, 비행기의 무게가 증가해도 활공각이 변하지 않는다는 것을 정확하게 이해하기란 쉽지 않다. 얼핏보기에는 유도항력이 증가하기 때문에 최대활공속도의 활공각역시 커져서 최대활공거리는 줄어들것처럼 여겨지지만 절대로 그렇지 않다. 왜냐하면 무게가 증가하면 받음각이 증가하므로 항력 뿐 아니라 양력도 그만큼 같이 증가하기 때문이다.

즉, 무게로 유도항력으로 늘어난만큼 양력도 같이 증가했기 때문에 양항비에는 변화가 없다는 것이다. 이것은 양항비를 구하는 식을 살펴봄으로써 확인할 수 있다.

여기서 분자 분모를 L로 나누면,

양항비가 가장 커질때는 분모가 가장 작을 때이다. 여기서 분모에 산술평균과 기하평균의 관계를 적용하여 최소가 되는 분모 값을 구해보면,



분모가 최소가 되는 값, 즉 양항비가 최대로 되는 값은 비행기의 무게와 상관없이 오로지 유해항력계수(CD), 유해항력의 작용면적(A), 날개면적(S), 날개가로폭 효율(e), 날개의 가로세로비(AR)의 영향을 받는다는 것을 알 수 있다. 결국 최대 양항비는 이렇게 비행기의 형상에만 영향을 받기 때문에 비행기가 바뀌지 않는 이상 최대 양항비는 항상 일정하다.

아래 그래프는 예전에 쓴 "양항비, 양력(LIFT)과 항력(DRAG)의 비(RATIO), 언제 최대가 될까? (수정)" 글에서 만들었던 양항비_항력_ 그래프.xlsx 를 가지고 비행기의 무게만 바꿔가지고 양항비가 어떻게 나오는지 실험해본 결과이다.


이 두개의 그래프 모두 CD*A는 0.3, SπeAR에는 0.5의 값을 사용하였는데,
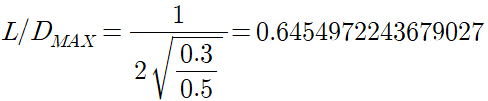
비행기의 무게가 1557이든, 1999이든 관계없이 모두 이론적인 양항비 최대값인 0.6454972243679027을 나타내고 있음을 알 수 있다.
그럼 최대 양항비가 일정한 것과 최대활공거리가 일정한 것은 무엇 때문일까? 논리적으로 하나씩 풀어나가보자!
아래 그림은 비행기가 활공중일때 비행기에 미치는 힘들을 벡터로 나타낸 것이다.

활공중일 때 비행기에 작용하는 모든 힘은 평형을 이루고 있음으로, 양력을 L, 중력을 W, 항력을 D로 놓았을때 다음과 같은 식이 성립한다.

위 식에서 알 수 있듯이 무게(W)는 모두 소거되고 오직 양항비(L/D)에 의해 활공각 θ가 변하는 것을 알 수 있다. 여기서 θ의 함수는 cot 함수임으로 활공각 θ가 커질수록 양항비는 감소한다.

따라서 반대로 양항비가 커질수록 활공각이 감소하여 활공거리는 늘어나게 된다는 사실을 알 수 있을 것이다.
비행기의 양항비가 곧 그 비행기의 활공거리를 결정하게 되는 것이다. 따라서 최대 양항비가 일정하면 최대활공거리도 일정하게 되는것이다.
자! 이제, 지금까지 살펴본 사실들을 토대로 결론을 내려보면,
활공거리는 오직 양항비의 영향을 받으며,
최대 양항비는 무게의 영향을 받지않고 비행기의 형상에 영향을 받는다.
따라서 최대 활공거리는 비행기가 동일하면 언제나 일정하다!
끝.
'비행 관련 기타' 카테고리의 다른 글
| 2021서울 ADEX, 무인기 시대의 서막을 알리다.(스압) (0) | 2021.10.24 |
|---|---|
| STANDARD RATE TURN 뱅크 계산식 분석 (7) | 2021.07.28 |
| Vg 다이어그램을 그려보자! (4) | 2021.06.16 |
| 양항비, 양력(LIFT)과 항력(DRAG)의 비(RATIO), 언제 최대가 될까? (수정) (8) | 2020.08.14 |
| 상반각(dihedral angle)에 대한 오류, 그리고 그것을 해결하는 Dihedral effect (21) | 2020.07.25 |






