| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- UAM
- 2007년 제4차 자가용조종사 변형
- 항공안전법
- ICAO Annex 14
- Lead Radial
- Best Glide Speed
- FPNM
- dutch roll
- 2007년 제3차 운송용조종사 변형
- annex14
- sideslip
- icao
- load factor
- dihedral effect
- 국제민간항공협약
- 13년도 공단 기출문제 변형
- Turn radius
- Propeller
- Today
- Total
비행사의 다이어리
양력이론 - 1 [공기의 유체적 특성] 본문
이 번 글부터는 양력이론에 대해서 다룰 텐데요,
제일먼저 살펴볼 것은 바로 '공기의 유체적 특성'입니다.
공기의 유체적 특성

유체라 하면 흔히 '액체'를 생각할 수도 있겠지만 공기(또는 대기)와 같은 '기체' 또한 '유체'입니다. 따라서 비록 눈에 잘 띄진 않지만 액체 에서 볼 수 있는 유체적 특성들을 기체에서도 볼 수 있습니다.
그 대표적인 특성이 바로 '점성' 입니다.
 |
 |
"점성(Viscosity)"
말 그대로 끈끈한 정도 입니다. 액체를 먼저 살펴 보면, 점성에 크기에 따라 어떤 건 물엿처럼 끈끈하니 잘 흐르지 않고, 어떤 것은 맑은 물 처럼 시원하게 잘 흐릅니다. 그리고 점성이 클수록 저항이 크게 나타나게 되는데요, 맑은 물을 막대로 저을 때 보다 끈끈한 꿀이나 물엿을 막대로 저을 때 더 잘 안 저어지는 것을 생각하면 될 것 같습니다.
그렇다고 맑은 물이 점성이 아예없는 것은 아닙니다.
이상적인 유체가 아닌 한 점성이 없는 유체는 없습니다. 맑은 물을 막대로 저을 때도 물이 막대주변에 흐른다는 느낌은 납니다.
 |
 |
공기도 마찬가지 입니다. 점성이 있습니다. 그래서 바람이 세계 부는 날 피부에 와 닿는 공기를 직접 느낄 수가 있는 것입니다. 피부나 털, 머리카락 표면에 달라붙은 끈끈한 공기입자가 주변 공기가 움직임으로써 '같이 움직이려는 힘'을 받기 때문이죠.
이 때, '그 힘'이 미치는 영역의 경계를 우리는 '경계층(Boundary Layer)'이라고 부릅니다. 그리고 '그 힘'을 좀 고상한 표현으로 '점성력'이라 하지요.
"경계층(Boundary Layer)",
즉, '경계층(Boundary Layer)'은 점성력이 미치는 영역과 미치지 않는 영역을 구분하는 경계입니다.

위 그림은 유속 u(0)로 흐르는 유체가 매끄러운 물체의 표면위에 흐르게 될 때 점성에 의하여 유속이 u(y)로 바뀌게된 것을 나타낸 그림입니다. 그림에서 점선은 경계층을 나타내며 이 경계층 아래 회색음영으로 표시된 면적이 점성력의 영향이 미치는 영역입니다. 보시다시피 이 영역 안에서는 점성에 의한 저항으로 인해 물체의 표면에 가까워질수록 일정하게 유속이 감소하는 모습을 볼 수 있습니다. 그리고 궁극적으로 물체표면에서는 속도가 0가 됩니다.

다만, 실제로는 아무리 매끄러운 물체표면이라도 미세한 요철이 있을 수 밖에 없기 때문에 그 만큼 경계층 내의 유체의 흐름을 방해하게 됩니다. 따라서 이때 나타나는 저항은 단순히 점성력에 의한 저항 뿐 아니라 마찰에 의한 저항도 같이 나타나게 되는 것입니다. 이 같은 저항들을 통틀어 '항력(Drag)'라고 부르는데요, 좀 더 구체적으로 여기서 나타난 점성 저항과 마찰 저항만을 통틀어 마찰항력(Skin friction drag)이라 일컫습니다.
한편, 경계층 밖에서는 점성의 영향이 거의 미치지 않고 물체표면 마찰에 의한 영향도 받지 않기 때문에 유속이 처음과 별 차이가 없이 균일하게 흐르는 모습을 볼 수 있는데요, 이 흐름을 자유흐름(Free stream)이라고 부릅니다. 즉, 이 영역에서는 점성에 의한 저항도, 마찰에 의한 저항도 없다고 볼 수 있습니다.

이러한 경계층은 유체의 흐름에 따라 뒤로 갈수록 점점 두꺼워 집니다. 그리고 어느 순간부터 경계층 내부의 일정한 흐름이 불규칙한 흐름으로 바뀌게 됩니다.
"층류(laminar flow)와 난류(turbulent flow)"

우리가 앞서 살펴본 경계층 내부의 유체의 흐름은 '층류(laminar flow)'일 때의 모습 입니다. 층류는 말 그대로 그 흐름이 얇은 층(laminar)을 이루며 각 층을 벗어나지 않고 일정하고 규칙적으로 나아가는 유체의 흐름을 말합니다. 경계층 밖의 유체와 물체표면위를 지나가는 초기 경계층 내 유체는 이러한 층류의 흐름을 보입니다.
그러나 경계층 내의 유체는 어느정도 물체표면 위를 지나가게 되면 각 층에서의 지속적인 속도차이가 누적되어 흐름의 상하 이동이 생기면서 섞이게 되고(Transition, 천이),
최종적으로는 예측할 수 없는 불규칙한 흐름인 '난류(turbulent flow)'가 나타나게 됩니다.

난류가 나타나게 되면 기본적으로 흐름의 상하이동이 있기 때문에 전반적인 흐름이 매끄럽지 못하고 경계층도 층류 일 때 보다 훨씬 두꺼워지며 항력도 급증하는 양상을 띄게됩니다.
그렇다면 난류는 언제 나타나게 될까요?
"레이놀즈 수(Reynolds number)"

난류가 나타나는 조건은 레이놀즈 수(Reynolds number)를 통해서 알 수 있습니다. 레이놀즈 수를 구하는 공식은 다음과 같습니다.

공식을 잘 살펴보면 난류가 언제 잘 나타나게 되는지 알 수 있습니다. 레이놀즈 수가 커질수록 난류가 되기 때문에 레이놀즈 수를 크게 만드는 요소를 살펴보면 되기 때문이죠.
그런데, 여기서도 난류를 만드는데 우리가 앞에서도 살펴본 '점성력'이 매우 중요한 위치를 차지하고 있다는 사실을 알 수 있습니다. 점성력이 레이놀즈 수의 분모를 구성하고 있기 때문입니다. 따라서 점성력이 작은 유체일수록 레이놀즈 수는 커집니다. 즉, 점도가 낮고 잘 흐르는 유체일수록 난류가되기 쉽고 점도가 높은 끈끈한 유체일수록 층류가 되기 쉽다는 말입니다.
위 영상을 보면, 점도가 높은 시럽 속에 담긴 잉크색소가 시럽이 움직이는 미세한 층을 따라 움직이기만 할 뿐 다른 곳으로 불규칙하게 퍼지지 않는다는것을 알 수 있습니다. 매우 안정적인 층류가 만들어졌기 때문입니다. 이와같이 점도가 높아질수록 층류는 뚜렷이 나타나게 됩니다.
 |
 |
<사진출처: Laminar and Turbulent Flow -CME330(YouTube)>
점도에 따른 층류와 난류의 차이는 우리 일상생활 속에서도 볼 수 있는데요, 위 사진처럼 점도가 높은 액체를 따를 때는 유선의 흐름이 끊기지 않고 길게 연장되는 모습을 볼 수 있지만, 점도가 낮은 액체를 따를 때는 유선이 흐트러지거나 흐름이 끊기는 모습을 종종 확인할 수 있습니다.
이 밖에 레이놀즈 수에 영향을 미치는 요소로는 '거리' 와 '속도'가 있습니다. 이 두가지 요소는 레이놀즈 수식에서 분자를 구성하고 있습니다.

'거리'에 대해서는, 이미 앞서 살펴본 바와 같이, 물체표면위를 흐르는 경계층 내의 층류 흐름이 뒤로 갈수록 난류 흐름로 변한다는 사실을 통해 알 수 있습니다. 즉, 물체표면의 길이가 짧으면 경계층내의 흐름이 난류로 변하기 전에 끝나겠지만 물체표면의 길이가 길면 경계층내의 흐름이 난류로 변할 때까지 이어질 수 있다는 말입니다. 따라서 유체가 흐르는 거리가 클수록 레이놀즈 수는 커집니다.

비행기의 날개의 세로길이가 짧은 것도 이와 무관하지 않습니다.
'속도'가 레이놀즈 수에 미치는 영향은 의외로 우리주변에서도 쉽게 관찰 할 수 있습니다. 대표적인 것이 바로 수도꼭지에서 나오는 물 입니다.
 |
 |
<사진출처: Laminar versus turbulent flow through a kitchen faucet(YouTube)>
수도를 충분히 약하게 틀면 수도꼭지에서는 유선이 일정하고 흐트러짐이 없는 매우 맑고 투명한 물줄기의 흐름을 볼 수 있습니다. '층류'입니다. 반면, 수도를 세계 틀면 물의 유속이 빨라지면서 유선이 흐트러져 불투명하고 어지럽게 움직이는 '난류'의 흐름을 볼 수 있습니다.
따라서 유체의 속도가 증가 할 수록 레이놀즈 수는 커진다고 볼 수 있습니다.
자, 지금까지 레이놀즈 수를 통해 층류와 난류의 관계를 살펴보고 난류가 어떤 조건에서 만들어 지는지에 대해 살펴보았습니다. 정리해 보면,
- 유체의 점도가 낮고,
- 유체가 표면을 따라 흐르는 길이가 길며,
- 유체가 흐르는 속도(유속)가 빠를때 난류가 잘 나타나게 됩니다.
그리고 이러한 난류가 경계층 안에 나타나게 되면, 앞에서 살펴보았듯이
- 유체의 흐름이 매끄럽지 못하게 되고,
- 경계층이 층류 일 때 보다 훨씬 두꺼워지며,
- 이로 인하여 항력도 급증하게 되는데요.
그런데, 공기는 유체들 중에서도 점도가 낮은 축에 속하며, 비행기는 양력을 얻기위해 빠른속도로 공기 속을 움직이기 때문에 유속이 빠릅니다. 따라서 공기라는 유체는 난류로 부터 결코 자유로울 수가 없습니다.
그렇다면 이와 같은 난류는 나쁘기만 한 것일까요?
"흐름의 박리(Flow separation)"

층류 경계층은 난류 경계층에 비해 항력이 작지만 그 두께가 매우 얇고 불안정 하여 경계층 내 국부적으로 유속이 충분치 못한 곳이 있거나 물체 표면의 굴곡 등에 의해 그 흐름이 급격하게 변하면 쉽게 박리된다는 치명적인 단점이 있습니다. 일단 경계층이 물체로부터 박리가 되면 박리가 된 쪽에는 유체가 흐르지 못하는 공간이 생기게 되고 이 공간의 압력 차이로 인해 결과적으로 큰 항력이 나타나게 됩니다.

이 때의 항력은 경계층과 물체표면사이의 점성이 만들어 내는 항력과는 근본적으로 다른 '압력항력(Pressure drag 또는 Form drag)'이며 그 영향력도 훨신 큰 편입니다.
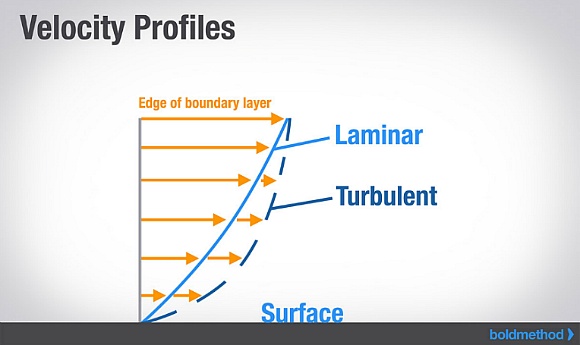
따라서 이와같은 흐름 박리에 의한 압력항력이 나타나지 않게 하기 위해서는 경계층의 박리를 막는 것이 중요한 포인트가 됩니다. 이때는 얇은 층류 경계층 보다는 마찰저항이 더 크더라도 경계층 내에 충분한 유속을 가지고 있어 흐름 박리에 잘 견디는 두터운 난류 경계층이 더 유용하게 쓰이게 됩니다.

실제로 골프공 같은 경우를 보면 표면에 여러군데에 홈 을 파여진 것을 볼 수 있는데요, 이것은 의도적으로 골프공 주변을 둘러싼 공기의 흐름을 교란시켜 난류 경계층 만들기 위함 입니다. 일단 두터운 난류 경계 층이 만들어지면, 마찰항력은 증가하겠지만, 층류였을때 보다 흐름 박리에 더 강해지고, 또 그 만큼 흐름 박리에 의한 압력항력도 줄일 수 있기 때문이죠.
이와같이 난류가 무조건 나쁘기만 한 것은 아닙니다. 경계층 안에 형성된 난류는 두터운 난류 경계층을 만들어 흐름 박리에 대항할 수 있도록 해줍니다. 다만 이것은 어디까지나 경계층 내에 존재하는 난류에 한해서라는 것을 염두에 두셨으면 합니다.
난류가 있는 곳에는 항상 기본적으로 항력이 뒤 따릅니다. 아래 영상을 보시면,
흐름이 박리되는 곳에서도 소용돌이 형태(Wake)의 난류가 나타나는 것을 볼 수 있습니다. 난류가 압력항력의 결과물로 나타난 것입니다. 이와같이 난류라는 것이 워낙 포괄적인 개념이다보니 단순히 난류 라고만 말한다면 충분히 헷갈릴 수 있습니다. 하지만 난류가 경계층 안쪽에 있을 때와 밖에 있을 때를 구분하면 어떤 난류가 흐름의 박리를 지연시켜주고 어떤 난류가 항력의 결과로서 나타나는지를 구분하실 수 있을 겁니다.
이로써 공기의 유체적 특성에 대해서 모두 살펴보았습니다.
다음 글에서도 계속해서 양력이론에 관해 다루겠습니다.
'비행기 조종사 학과 > 비행원리' 카테고리의 다른 글
| 비행기에 미치는 힘 - 2 [양력(Lift)와 항력(Drag)] (0) | 2020.07.31 |
|---|---|
| 비행기에 미치는 힘 - 1 (0) | 2020.07.29 |
| 양력의 3 차원적 문제 (17) | 2020.07.28 |
| 양력이론 - 2 [작용과 반작용, 베르누이의 법칙, 에어포일, AOA] (26) | 2020.07.27 |
| 대기(Atmosphere) (4) | 2020.07.27 |





