| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- dutch roll
- Lead Radial
- Turn radius
- Best Glide Speed
- load factor
- ICAO Annex 14
- 국제민간항공협약
- UAM
- 2007년 제3차 운송용조종사 변형
- 13년도 공단 기출문제 변형
- 항공안전법
- annex14
- 2007년 제4차 자가용조종사 변형
- icao
- Propeller
- sideslip
- FPNM
- dihedral effect
- Today
- Total
비행사의 다이어리
양력이론 - 2 [작용과 반작용, 베르누이의 법칙, 에어포일, AOA] 본문
이 번 글에서도 양력이론에 대해 계속 살펴보겠습니다.
먼 저번 글에서 우리는 유체의 특성을 배웠고 이 번 글에서는 이러한 유체가 어떻게 항공기가 뜰 수 있는 양력(Lift)를 만들어 낼 수 있는지 알아볼 것입니다.
실제로 유체가 양력을 만드는 과정을 이해하는 것은 매우 복잡하고 어렵습니다. 따라서 여기서는 양력을 직관적으로 설명할 수 있는 대표적인 이론 두 가지를 살펴볼텐데요. 첫 번째는 뉴턴의 제3법칙인 '작용과 반작용의 법칙', 그리고 두번째는 '베르누이의 법칙'입니다.
"작용과 반작용의 법칙"
작용과 반작용, 학창시절 물리시간에 한번쯤 들어보셨을 겁니다. 주로 로케트 발사 예와 함께 언급됩니다. 로케트의 추진체가 아래로 분사되면 로케트는 그 반작용으로 위로 떠오르게 됩니다.
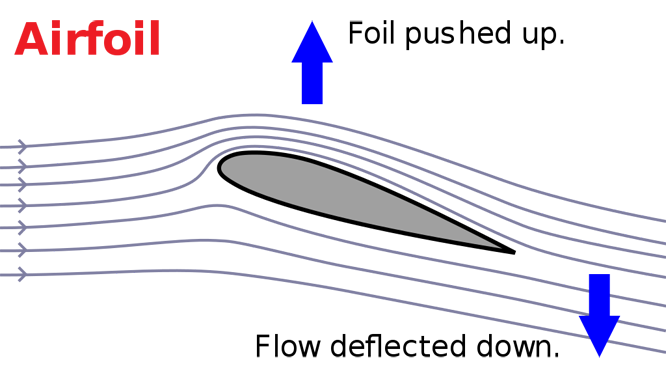
자, 그럼 이번엔 양력을 같은 틀 안에서 접근해 봅시다. 비행기가 공중에 떠 있으려면, 로케트의 추진체와 같이, 뭔가 아래로 작용하는 힘이 존재해야 할 것입니다. 즉, 위로 떠받치는 힘인 양력이 존재한다면 양력과 크기가 같은 반대의 힘이 반드시 존재해야 한다는 것입니다. 그 힘에 의해 나타난 것이 바로 비행기 날개에서 생기는 하강하는 공기흐름인 DOWN WASH 입니다. 이 DOWN WASH에 대해서는 뒤에서 좀 더 자세히 살펴 보겠습니다.
어째든 정리하면, 양력은 큰 틀에서는 유체가 DOWN WASH를 만들어 내는 힘의 반작용으로 나타난 결과물이라고 볼 수 있습니다.
"베르누이의 법칙(Bernoulli's principle)"
이번엔 베르누이의 법칙을 통해 작은 틀에서 양력이 나타나는 원리를 살펴보겠습니다.

베르누이의 법칙은 기본적으로 지름이 변하는 관, 즉 벤추리 관(Venturi tube) 속을 흐르는 유체를 대상으로 합니다. 위 그림 처럼 벤추리 관을 채우고 있는 유체가 흐른다고 생각해봅시다. 이 때 관속으로 들어가는 유체의 양과 관 밖으로 나가는 유체의 양이 같다고 본다면, 관 속에서도 들어가고 나갈때와 동일한 양의 유체가 지나간다고 생각해 볼 수 있을 것입니다. 즉, 다시말해 관의 지름이 커지든 작아지든 관계없이 관 속에는 항상 들어가고 나가는 양 만큼의 유체가 흐른다는 것입니다.

이렇게 흐르는 유체의 양이 지름이 변하는 관속에서 계속 일정하게 유지되기 위해서는 유속이 변해야 합니다. 만약 유체가 통과하는 관의 지름이 크다면 유속은 상대적으로 느려져야 흐르는 양을 맞출 수 있을 것이고 반대로 관의 지름이 작다면 유속이 상대적으로 빨라져야 흐르는 양을 일정하게 맞출 수 있을 것입니다(V1 < V2).

요즘은 학교에서도 '위치 에너지' 대신 '퍼텐셜 에너지'란 표현을 씁니다. *_*
자, 이렇게 유체의 속도가 변하게 되면 유체의 운동 에너지도 변하게 되기 때문에 '역학적 에너지 보존법칙'에 따라 다른 무언가의 에너지 크기도 변하게 됩니다. 높은 곳에 있는 물체가 아래로 떨어질때 운동 에너지가 증가 한 만큼 위치 에너지가 감소하듯이 말입니다. 그래서 유체의 운동 에너지가 증가하게 되면 '퍼텐셜 에너지(potential energy)'가 감소하게 되는데요, 바로 이 퍼텐셜 에너지 변화로 인해서 '압력'이 감소하게 되는 것입니다.
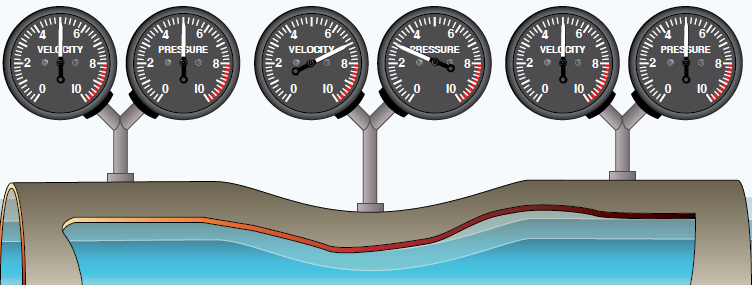
그래서 베르누이 법칙의 결론은, "유체의 속도가 증가하면 동시에 그 압력은 떨어진다" 입니다.
중요한 건 지금 살펴본 "작용 반작용의 법칙", 그리고 "베르누이 법칙"은 서로 동떨어진 법칙이 아니라는 사실입니다. 작용과 반작용의 법칙은 '힘'을 다루고 베르누이 법칙은 '압력'을 다룹니다. 따라서 하나는 양력을 큰 틀에서 통채로 해석한 것이고 다른 하나는 작은 틀에서 디테일하게 해석한 것입니다.
So both "Bernoulli" and "Newton" are correct. Integrating the effects of either the pressure or the velocity determines the aerodynamic force on an object. We can use equations developed by each of them to determine the magnitude and direction of the aerodynamic force. (인용출처: NASA Glenn Research Center)
그럼 이제 이 법칙들이 구체적으로 어떻게 항공기 날개에 적용되어 양력을 발생하는지 살펴보도록 하겠습니다.
"에어포일(Airfoil)",


항공기 날개의 단면은 에어포일(airfoil)의 구조로 되어있습니다. 에어포일이란 공기의 흐름으로부터 공기역학적 효과를 얻기 위해 설계된 구조를 말하는데요. 에어포일에서 나타나는 대표적인 공기역학적 효과가 바로 '양력(Lift)'입니다.


에어포일에서 양력이 만들어지는 과정은 간단합니다. 에어포일 전면에 나타나는 상승 흐름인 UP WASH는 에어포일의 형상에 의해 아래로 힘을 받게되어 하강 흐름인 DOWN WASH로 변화하면서 그 반작용으로 위로 작용하는 힘, 즉 양력을 만들어내게 됩니다(작용 반작용의 법칙). 또는 에어포일의 윗면에 흐르는 공기의 속도가 아랫면보다 빨라지면 에어포일 윗면에서는 아랫면보다 낮은 압력이 아랫면보다 낮아지기 때문에 그 압력차로 떠오르게되는 양력이 만들어진다고도 볼 수 있는데요(베르누이의 법칙). 중요한 것은 '에어포일이 그 주변에 흐르는 공기흐름의 방향과 속력을 변화 시킨다'는 점입니다.

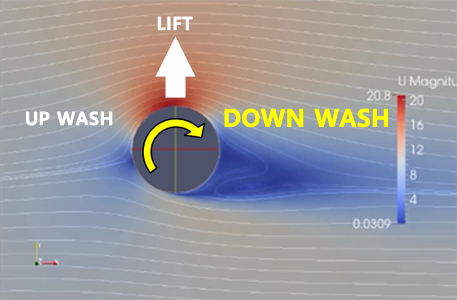
이와같은 현상은 흐르는 유체속에서 회전하는 원형 물체에서도 나타납니다. 위 영상과 사진에서 처럼 흐르는 유체속에서 회전하는 원형물체는 물체 주변의 유체흐름을 변화시켜 DOWN WASH를 만들어 냅니다. 그리고 DOWN WASH가 만들어지는 물체의 표면에서 유속이 가장 빠르다는 것을 알 수 있습니다. 이러한 유체흐름의 속도 변화와 그로 인한 DOWN WASH를 만들어낸 힘에 의해 에어포일에서의 양력과 같은 힘을 발생시키는데요, 이것을 'Magnus Force'라고 합니다. 그래서 아래 영상에서 처럼 회전하는 원통을 비행기의 날개대신 사용할 수도 있습니다.
즉, 유체흐름의 속도 변화와 그에 따른 DOWN WASH가 나타다면 양력을 얻을 수 있다는 결론이 나옵니다.
그래서 일반적인 에어포일에는 그와같은 목적을 달성하기 위해 윗면과 아랫면의 비 대칭적인 곡률을 만들어 주는 '캠버(Camber)'라는 설계를 적용합니다.

캠버는 보통 시위선(Chord line) 위쪽에 적용되어 에어포일의 윗면을 아랫면보다 더 굴곡지게 만듭니다. 이렇게 하면 에어포일의 윗면을 흐르는 공기흐름을 효과적으로 가속시켜주며 동시에 공기가 굴곡된 형태를 따라흐르면서 자연히 DOWN WASH가 나타나게 되며 속도가 바뀌게 됩니다. 그리고 에어포일 윗면과 아랫면의 속도 차이가 커지고 DOWN WASH 커질수록 그만큼 더 많은 양력을 얻을 수 있겠죠.
하지만 에어포일이 양력을 발생시키기 위해 반드시 캠버가 필요한 것은 아닙니다.
"받음각(Angle Of Attack; AOA)"


에어포일을 향해 다가오는 공기의 자유흐름(Freestream), 또는 상대풍(Relative wind)과 에어포일의 시위선 사이에 적절한 각을 이루면, 캠버가 적용되지 않은 대칭형 에어포일(symmetrical airfoil)에서도 양력을 얻을 수 있습니다. 이 때의 에어포일로 입사되는 자유흐름의 방향 과 에어포일의 시위선 사이에 각을 '받음각(Angle of attack, AOA)'이라고 하는데요, 위 영상처럼 받음각이 에어포일 윗면의 공기흐름을 가속시켜주고 동시에 DOWN WASH의 양을 증가시켜주기 때문에 캠버 적용과 관계없이 양력을 얻을 수 있는 것 입니다.

그래서 바람을 적절한 받음각으로 받으면 종이비행기의 평평한 날개에서도 양력을 얻을 수 있습니다. 그리고 아래 목록과 같은 특이한 형태의 에어포일도 나올 수 있는 것이죠.

자, 이렇게 결국 에어포일에서 나타나는 양력은 '작용과 반작용' 그리고 '베르누이의 법칙'을 통해 이해할 수 있습니다. 여기서 핵심은, 에어포일 윗면과 아랫면의 속도차를 만든다는 것, 그리고 그로인해 DOWN WASH를 만드는 어떤 힘이 양력의 반작용으로 발생한다는 점 입니다. 캠버를 적용하든 받음각을 사용하든 일단 이렇게 속도 차이로 DOWN WASH가 나타나게 만들어 놓으면 베르누이의 법칙을 따르든 작용 반작용을 따르든 어째든 양력이 만들어지기 때문입니다.
그럼, 이렇게 만들어진 양력은 에어포일의 어느 지점에서 작용할까요?

에어포일에 흐르는 공기의 속도에 의해 압력의 변화가 생길때 모든 위치에서 똑같은 크기의 압력변화가 생기지 않을 것입니다. 에어포일의 구간구간 마다 속도 차이가 다 다르기 때문입니다. 이렇게 에어포일 주변의 각기 다른 모든 압력들을 하나의 압력으로 표현했을때 그 압력의 위치를 '압력중심(Center of pressure, CP)'이라고 하는데요, 양력은 바로 이 압력중심에 작용하는 것으로 봅니다. 무게가 무게중심에 작용한다는 것과 비슷하게 생각하시면 될 것 같습니다.
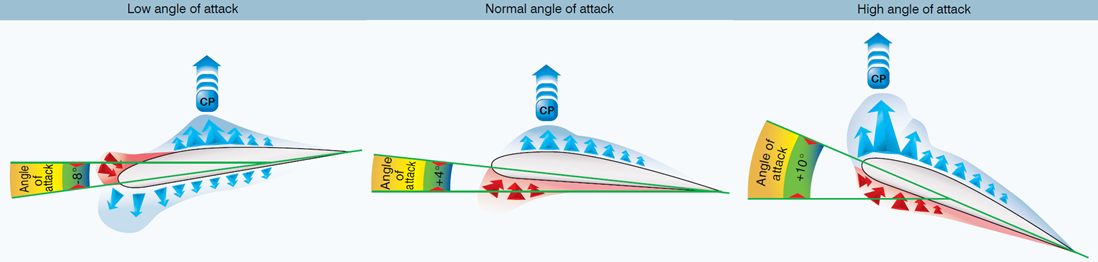
그런데 이 압력중심은 일반적인 에어포일의 경우 받음각에 따라 변화하기 때문에 양력이 에어포일에 작용하는 위치도 달라지게 됩니다. 위 그림처럼 캠버가 적용된 일반적인 에어포일에서 받음각이 증가하면 압력중심은 전진하고, 받음각이 감소하면 압력중심은 후퇴하게 됩니다.
반면 대칭형 에어포일(symmetrical airfoil)의 경우 특이하게도 받음각이 변해도 압력중심의 위치는 변하지 않습니다.
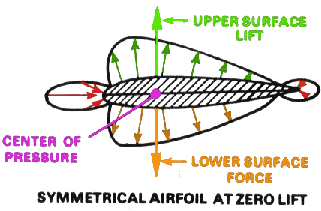 |
 |
<그림출처: Dynamic Flight, Inc.>
하지만 이것은 어디까지나 대칭형 에어포일에만 해당되는 특수한 경우입니다.
따라서 통상적으로는 받음각이 증가하면 압력중심은 앞으로 이동하고, 감소하면 압력중심은 뒤로 이동 하는것으로 여깁니다. 그리고 이와같은 받음각에 따른 압력중심의 변화는, 나중에 살펴볼테지만, 항공기의 안정성과 관련이 있음으로 꼭 기억해 두시기 바랍니다.
.
.
지금까지 공기의 특성, 베르누이의 법칙, 에어포일의 특성, 뉴턴의 운동법칙 등을 통해 양력의 기본적인 이론들을 살펴보았습니다. 앞에서도 말씀드렸듯이 이 양력이라는 주제가 사실 이렇게 간단하게 설명할 수 있는 문제가 아닙니다. 다만 조종사의 입장에서 필요한 정보만, 최대한 직관적으로, 단순하게 이해할 수 있게 접근해 보려고 노력했습니다. 참고로 NASA 홈페이지에 우리가 잘 못 이해하고 있는 양력이론들에 관한 정보들을 알려주고 있습니다.
(NASA Glenn Research Center) Guide to Aerodynamics #Lift
Guide to Aerodynamics - Glenn Research Center | NASA
Aerodynamics is the study of forces and the resulting motion of objects through the air. What is Aerodynamics? The word comes from two Greek words: aerios, concerning the air, and dynamis, which means force. Aerodynamics is the study of forces
www1.grc.nasa.gov
Equal Transit Theory Interactive - Glenn Research Center | NASA
There are many theories of how lift is generated. Unfortunately, many of the theories found in encyclopedias, on web sites, and even in some textbooks
www1.grc.nasa.gov
Skipping Stone Theory Interactive - Glenn Research Center | NASA
Incorrect Theories of Lift There are many theories of how lift is generated. Unfortunately, many of the theories found in encyclopedias, on web sites, and
www1.grc.nasa.gov
Venturi Theory - Glenn Research Center | NASA
There are many theories of how lift is generated. Unfortunately, many of the theories found in encyclopedias, on web sites, and even in some textbooks are
www1.grc.nasa.gov
같이 참고 해서 보시면 양력이론을 이해하시는데 많은 도움이 되실 겁니다.
혹시 영어가 부담스러우시면, '나무위키(링크클릭)'에서 해당내용을 참조 하실 수 있습니다.
'비행기 조종사 학과 > 비행원리' 카테고리의 다른 글
| 비행기에 미치는 힘 - 2 [양력(Lift)와 항력(Drag)] (0) | 2020.07.31 |
|---|---|
| 비행기에 미치는 힘 - 1 (0) | 2020.07.29 |
| 양력의 3 차원적 문제 (17) | 2020.07.28 |
| 양력이론 - 1 [공기의 유체적 특성] (6) | 2020.07.27 |
| 대기(Atmosphere) (4) | 2020.07.27 |