| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 2007년 제3차 운송용조종사 변형
- dihedral effect
- 항공안전법
- sideslip
- Lead Radial
- dutch roll
- 2007년 제4차 자가용조종사 변형
- load factor
- 13년도 공단 기출문제 변형
- Propeller
- 국제민간항공협약
- annex14
- FPNM
- icao
- Best Glide Speed
- UAM
- Turn radius
- ICAO Annex 14
- Today
- Total
비행사의 다이어리
양력의 3 차원적 문제 본문
이 번글 에서는 앞서 2차원적인 면에서 '에어포일(airfoil)'만을 가지고 살펴 보았던 양력이론이 현실의 3차원적인 '날개(wing)'에 적용되면 어떻게 되는지 알아 보겠습니다.
"날개의 양력",

에어포일이 2차원에 존재하는 형상이었다면 에어포일이 모인 날개는 3차원에 존재하는 형상입니다. 그래서 기본적으로 에어포일의 양력에 영향을 미치는 요소들이 날개에도 영향을 미치게 됩니다. 뿐만 아니라 앞서 밀도고도에서 살펴봤듯이 대기의 상태도 날개의 양력에 영향을 줍니다.
자 그럼, 지금까지 살펴본 내용들을 토대로 날개의 양력에 영향을 미치는 요소들에는 어떤것들이 있는지 한번 정리해 봅시다.
첫번째, 양력의 영향을 미치는 요소로 '밀도고도'에서 살펴보았던 '공기의 밀도'가 있었습니다.

<질량 두배 = 운동 에너지 두배>
유체의 질량(밀도)이 커지면 그만큼 유체의 운동 에너지도 비례하여 커지게 됩니다.

<질량 두배 = 운동 에너지 차이 두배>
그 말은, 속도 변화에 따른 운동 에너지의 변화량 역시 커진다는 말인데요, 따라서 압력의 변화 역시 커지게 됩니다(베르누이의 법칙). 이렇게 대기의 밀도가 증가하면 속도차이에 따른 압력차이가 더욱 커지기 때문에 양력은 증가하게 됩니다.
두번째, '공기 흐름의 속도' 입니다.

<속도 두배 = 운동에너지 네배>
유체의 속도가 빨라지면 그만큼 유체의 운동에너지도 제곱에 비례하여 커지게 됩니다.
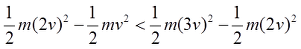
<속도 차 동일, 2V - V = 3V - 2V = V>
이 때 전체적인 공기 흐름속도가 커지면 똑같은 속도 차이라도 운동에너지의 차이는 더 커지게 됩니다. 그리고 그 만큼 압력차이도 더 많이 생기게 되는 것이구요. 따라서 양력은 증가하게 됩니다.
세번째, '에어포일의 형상'과 '받음각' 입니다.


앞서 '에어포일' 관련 글 에서 보았듯이 에어포일 형상 설계시 시위선 위쪽으로 캠버를 주면 양력은 증가하고 또한 에어포일에 입사되는 공기의 흐름에 받음각을 주었을때도 양력은 증가합니다.
마지막으로, '날개면적' 입니다.

날개는 수많은 에어포일이 모여 만들어진 구조입니다. 날개면적이 넓어지면 넓어질수록 에어포일이 그만큼 커지거나 많아지기 때문에 양력은 증가하게 됩니다.
이와같이 날개의 양력에는 공기의 밀도, 속도, 에어포일 형상과 받음각, 날개면적 등이 영향을 미칩니다. 따라서 이를 토대로 아래와 같은 양력 공식을 이끌어 낼 수 있습니다.

여기서,
- L 은 양력,
- ρ 은 공기의 밀도를,
- V 은 공기의 자유흐름의 속도, 즉, 비행기의 대기속도로 볼 수 있습니다.
- CL 은 양력계수로 에어포일의 형상과 받음각에 영향을 받습니다.
- S 는 면적을 나타냅니다.
이렇게 3차원의 날개를 2차원의 에어포일의 집합으로 가정하여 각 에어포일이 만드는 양력을 면적으로 합산한 식으로 깔끔하게 양력을 얻으면 좋겠지만, 현실은 그렇지 않습니다. 3차원의 유체 흐름은 2차원과는 달리 더 많은 변수가 있기 때문이죠.

"3차원적 문제",
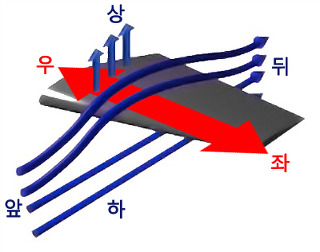

2차원 평면이 아닌 3차원 공간상에서는 공기는 '앞뒤상하' 뿐 아니라 '좌우'로도 흐를수 있습니다. 특히 날개의 윗면과 아랫면이 개방되어 있는 날개끝단에서 날개윗면과 아랫면의 압력차이로 인하여 아랫면의 상대적으로 높은압력의 공기가 윗면으로 이동하는 흐름이 발생하게 되는데요, 이 흐름이 날개 앞전에서 뒷전으로 흐르는 흐름에 더해져 일종의 소용돌이형태의 흐름(와류)이 만들어집니다.
이것을 'Wing tip vortex' 라고 합니다.

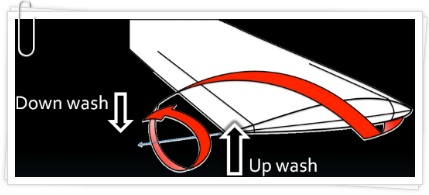
이렇게 Wing tip vortex 가 발생하게 되면 날개 아랫면에서 높은 압력으로 날개를 받쳐주어야 할 공기가 옆으로 새 버리는 형상이 되어버리므로 날개의 양력은 감소하게 됩니다. 그리고 이렇게 새어버린 공기는 날개를 떠 받치려던 힘으로 날개 밖에서 '상승하는 흐름(Up wash)'을 이루게 되며, 이 후 다시 압력이 낮은 날개 윗면으로 빨려들어가 날개 안쪽에서 '하강하는 흐름(Down wash)'을 이루게 되고, 이와같은 흐름(Up/Down wash)은 Wing tip vortex 를 따라 쭉 계속 이어지게 됩니다(Wing tip vortices).
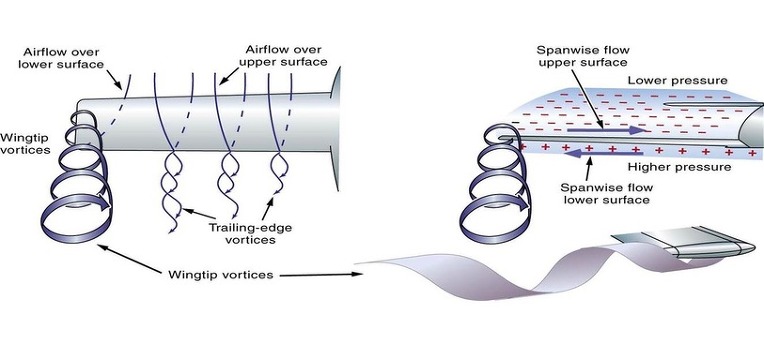
따라서 이렇게 만들어진 Down wash는 비록 날개 안쪽에 존재하더라도 양력의 반작용과는 관련이 없기 때문에 양력의 발생과는 상관이 없는 Down wash 입니다. 양력의 발생과 무관하기 때문에 이와같은 Down wash를 경우에 따라서는 'Induced down wash' 라고 부르기도 합니다.
 |
 |
<Wing tip vortex 발생하였을 때(좌)와 그렇지 않았을 때(우) 동일한 양력을 발생했을 경우 필요한 받음각(AOA)>
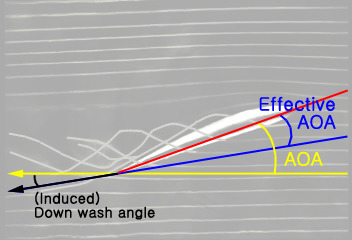
결국은, 날개 아랫면을 흐르면서 양력을 만드는 일을 해야할 공기흐름이 날개 윗면으로 올라와 양력을 만들어내는 대신 소용돌이(vortex)를 만드는 일을 했기 때문에 양력이 감소했다고 볼 수 있는데요, 이렇게 양력이 감소하게 되면 동일한 양력을 유지하기 위해서는 더 큰 받음각(Angle Of Attack)이 필요하게 됩니다.
그런데 여기서 역으로 양력손실이 발생하지 않았다면 동일한 양력을 얻는데 더 작은 받음각이 필요하겠지요. 즉, 전체 받음각에서 실제로 양력에 영향을 주는 받음각은 더 작다는 말입니다. 이와같이 실제로 양력에 영향을 주는 받음각을 '유효 받음각(Effective AOA)'이라고 합니다.
이와같이 Wing tip vortex가 발생하였을 때 양력은 일반적인 받음각이 아닌 '유효 받음각'의 영향을 받게되는데요, 문제는 유효 받음각을 이루는 공기의 흐름이 기울어져 있다는 사실입니다.
 |
 |
<Induced down wash에 의해 뒤로 기울어진 양력, 더 이상 상대풍에 수직이 아니기 때문에 양력으로 볼 수 없다>
이렇게 공기의 흐름이 기울어지게 된 것은 양력의 생성에 관여하지 않는 Induced down wash 가 나타나게 되므로써 날개에 작용하는 공기의 흐름이 변화했기 때문이라고 해석할 수 있습니다. 그러므로 위 그림처럼 Induced down wash 에 의해 실제로 작용하게 되는 공기의 흐름은 θ만큼의 기울기를 가지게 되므로 여기서 기존에 나타나던 양력도 θ만큼 기울어지게 됩니다. 따라서 이렇게 소위 기울어진 양력은 항력으로 작용하는 수평성분을 가지게 되는데요, 이 항력성분을 '유도항력(Induced Drag)'이라고 합니다.
이와같이 날개끝단에서 발생하는 Wing tip vortex 는 양력을 감소시키고 유도항력을 증가시키기 때문에 날개를 설계할때는 Wing tip vortex 에 대한 대책이 필요합니다.
"날개 끝 와류(Wing tip vortex)에 대한 대책",

제일먼저 생각해 볼 수 있는 대책은 바로 날개를 길게 만들어 날개 끝단을 최대한 멀리 두는 방법을 생각해 볼 수 있을 것입니다.

폭이좁고 긴 날개를 가로세로비(Aspect ratio)가 큰 날개라고 말하는데요, 가로세로비는 날개길이(span)를 시위(chord)길이로 나눈 값 입니다.
 |
 |
위 그림에 나타나 있듯이 Wing tip vortex 로 인한 down wash는 날개 끝단에서 멀어 질수록 약해지기 때문에 가로세로비가 큰 날개 일수록 유도항력이 작고 그로인한 양력손실도 적습니다.
그 다음으로 생각해 볼 수 있는 대책은 날개 끝단에 장애물을 설치하여 날개 아랫면에서 넘어오는 공기흐름을 차단하는 방법 입니다.


이와같은 목적으로 날개 끝단에 설치하는 장애물을 'Winglet' 이라고 합니다. Winglet 은 wing tip vortex 를 감소시켜줄 뿐 아니라 발생위치를 날개로 부터 어느정도 떨어뜨려 놓기때문에 그만큼 날개에 wing tip vortex 영향을 덜 받게 해줍니다.
그 밖에 대책으로 날개 끝으로 갈수록 날개윗면과 아랫면의 압력차를 서서히 줄여주여 날개끝에서 압력차가 작게 만드는 방법이 있습니다.

대표적으로 날개의 '테이퍼(Taper) 설계'를 들 수 있는데요, 테이퍼 설계는 'taper'라는 명칭 그대로 날개 끝으로 갈 수록 날개를 작게 만들어 날개를 뾰족한 형태로 만들어주는 것 입니다.

위 그림처럼 날개에 테이퍼를 극단적으로 주었을 때 날개 끝단은 '점'이 되기 때문에 날개 끝단에서의 양력은 0 이 되고 압력차도 0 이 됩니다. 그리고 끝단에서 부터 서서히 날개가 커지므로 날개 크기에 따라 각 부분별 압력차도 서서히 난다는 말 입니다. 따라서 압력이 급격하게 변하지 않고 서서히 변하기 때문에 날개 끝단으로 흐르는 공기의 흐름도 완만한 양상을 띠게되어 wing tip vortex 는 약해집니다.
다만 이렇게 되면 날개 끝으로 갈 수록 양력이 작아지는 문제가 생기게 됩니다.

따라서 실제 테이퍼 설계시에는 날개의 양력과 wing tip vortex 에 의한 손해를 어느정도 선에서 타협해야 하기 때문에 대부분의 테이퍼 형 날개는 완만한 사다리꼴 형상을 하고 있습니다.
자, 이렇게 이번 글에서는 날개의 양력과 3차원 공간이라 발생하는 wing tip vortex 문제에 대해 살펴보았습니다.
마지막으로 정리하면,
- 날개에서 발생하는 양력은 공기의 밀도 와 속도, 그리고 에어포일의 형상 및 받음각, 날개면적 등에 영향을 받는 사실을 알았고,
- 날개끝에서는 날개 윗면과 아랫면의 압력차로 인해 소용돌이의 흐름인 wing tip vortex 현상이 나타나는 것을 알았습니다.
- 그리고 이러한 wing tip vortex 는 날개주변 공기의 흐름을 변화시켜 양력을 감소시키고 항력(유도항력)을 증가시키기 때문에,
- 날개의 가로세로비를 크게하거나, 끝단에 winglet 을 설계하거나, 테이퍼 설계를 적용 등의 조치를 취한다는 것을 알았습니다.
다음 글에서는 "비행기에 미치는 힘"에 대해 살펴보겠습니다.
'비행기 조종사 학과 > 비행원리' 카테고리의 다른 글
| 비행기에 미치는 힘 - 2 [양력(Lift)와 항력(Drag)] (0) | 2020.07.31 |
|---|---|
| 비행기에 미치는 힘 - 1 (0) | 2020.07.29 |
| 양력이론 - 2 [작용과 반작용, 베르누이의 법칙, 에어포일, AOA] (26) | 2020.07.27 |
| 양력이론 - 1 [공기의 유체적 특성] (6) | 2020.07.27 |
| 대기(Atmosphere) (4) | 2020.07.27 |





